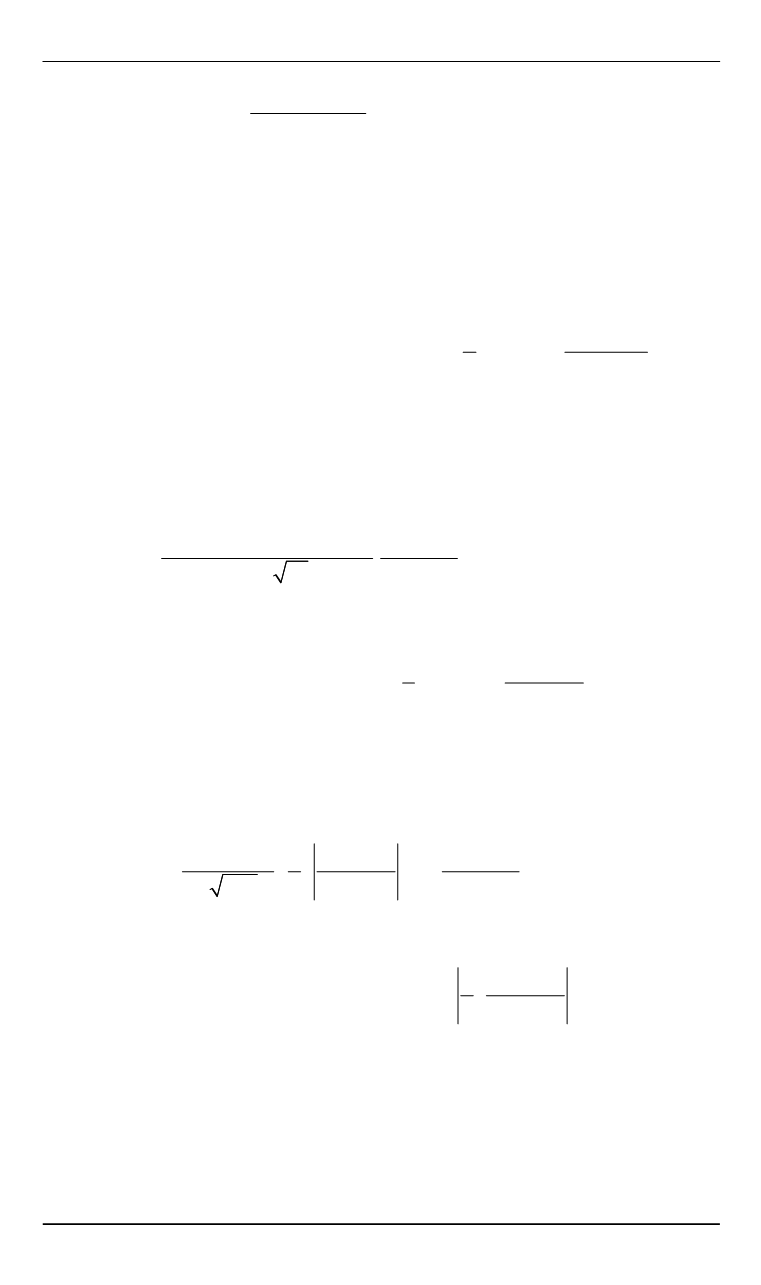
Моделирование волновой динамики стратифицированных сред
13
2
2
0
3/2
( )
( , ) ( , ).
( )
n j
n
j
n
j
j
n j
f
T
z
z
При
n
r c t
стационарные точки первого интеграла сливаются и
асимптотика интеграла оказывается зависящей от того, где достига-
ется максимум групповой скорости
( ).
n
c k
Если
0,
f
то для типич-
ных профилей
2
( )
N z
максимум будет в единственной точке
0.
В окрестности этой точки фазовая функция допускает разложение
2
3
2
1
( )
( )
(
)(
)
(
)
...
6
n
n
n
n
c
k r
k t
r
t k
r c t
k
t
где
( ),
( ).
n
n
n n
c c
Аппроксимируя фазовую функцию кубическим полиномом и за-
меняя внеэкспоненциальный множитель под знаком интеграла его
выражением при
,
k
находим
2
2
0
3/2
3/2
exp / 4 (
)
( , ) ( , ) ,
4 2
n
n
n
n
n
n
i
i
r
t
f
W
z
z
Z
r
где
2
3
2
1
( )
exp (
)(
) (
)
.
6
n
n
c
Z
i k
r c t
k
t
dk
Данный интеграл выражается через функцию Эйри
( ),
Ai
что
дает следующую асимптотику волнового поля в окрестности волно-
вого фронта:
1/3
2
2 2
0
0
2
3/2
exp( / 4) 1
( )
( , , , )
( , ) ( , ) ,
2
2 2
n
n
n
n
n
n
i
c
f
W r z z t
t
z
z
Y
r
где
1/3
2
2
1
( )
exp (
)
(
) /
.
2
n
n
n
c
Y
i
r
t Ai r c t
t
Проведенные по этим формулам численные расчеты показывают,
что для типичных длин внутренних гравитационных волн, характер-
ных для реального океана вдали от полярных зон, учет влияния вра-
щения Земли не вносит существенную поправку в дальние волновые
поля и его необходимо делать только для исследования волновых
возмущений в высоких широтах Мирового океана [10,11].


