Моделирование волновой динамики стратифицированных сред
23
скими частотами
N
и
N
качественно (при
N
количественно)
не меняется. Физически абсурдным также является приближение
Буссинеска в сжимаемой среде [2, 9]. В этом случае
0
A
N
и, следо-
вательно,
,
A
N N
что невозможно в устойчивых средах.
Дисперсионная кривая имеет две ветви (рис. 5) и качественно сов-
падает c дисперсионной кривой, изображенной на рис. 1, однако верх-
няя и нижняя границы диапазона запирания искажены. Поверхности
равных фаз при
N
принимают форму двухполостных
гиперболоидов вращения (рис. 6). Отметим, что в сжимаемой среде
0
волновое число
k
не зависит от угла
(изотропный случай):
2
2
1
) (
A
N
c
k
,
где
(2 ),
A
N g c
и поэтому анизотропия среды проявляется лишь в
появлении множителя
2
exp
2
gz c
в уравнении (27).
В заключение отметим, что при изучении внутренних гравитаци-
онных волн в океане обычно используют модель несжимаемой среды и
приближение Буссинеска. В этом приближении уравнение (26) сводится
не к уравнению Гельмгольца, а к уравнению Лапласа, так что волнового
распространения нет и среда движется синфазно, как при колебании тел
в несжимаемой однородной среде [2]. Однако при
N
между обла-
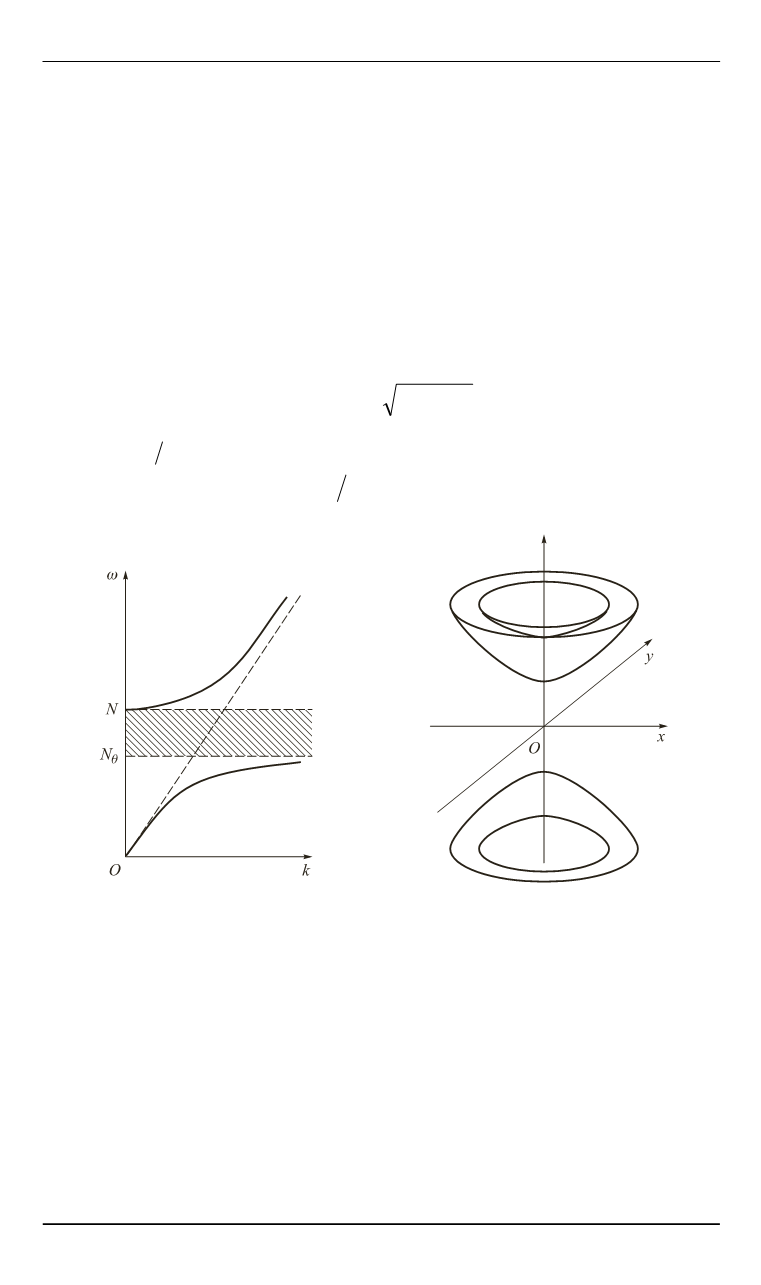
Рис. 5. Гравитационная ветвь дис-
персионных кривых
( )
k
аку-
стико-гравитационных волн в при-
ближении Буссинеска в сжимаемой
стратифицированной среде
Рис. 6. Гравитационная ветвь вол-
новых фронтов акустико-грави-
тационных волн в приближении
Буссинеска в сжимаемой страти-
фицированной среде


