Моделирование волновой динамики стратифицированных сред
21
звуковых волн. При
A
N
эллипсы становятся все более сплюсну-
тыми в вертикальном направлении. При
N
фронты представляют
собой семейство однополостных гиперболоидов вращения с общей
асимптотой под углом
arcsin( / ),
N
зависящим от частоты
(рис. 3,
б
). При
поле синфазно и экспоненциально убывает
при удалении от источника. Внутри конуса (при
)
поле осцил-
лирующее, гребни волн «удаляются» от конуса
.
На конусе
поле гармонического точечного источника имеет корневую особен-
ность
1
2
2
2
2
4
( )
.
sin
sin
A
NR
N
Если размеры ис-
точника конечные, то особенность не возникает, но поле в основном
сосредоточено в узкой области вблизи этого конуса, имеющей попе-
речные размеры, близкие к размерам источника.
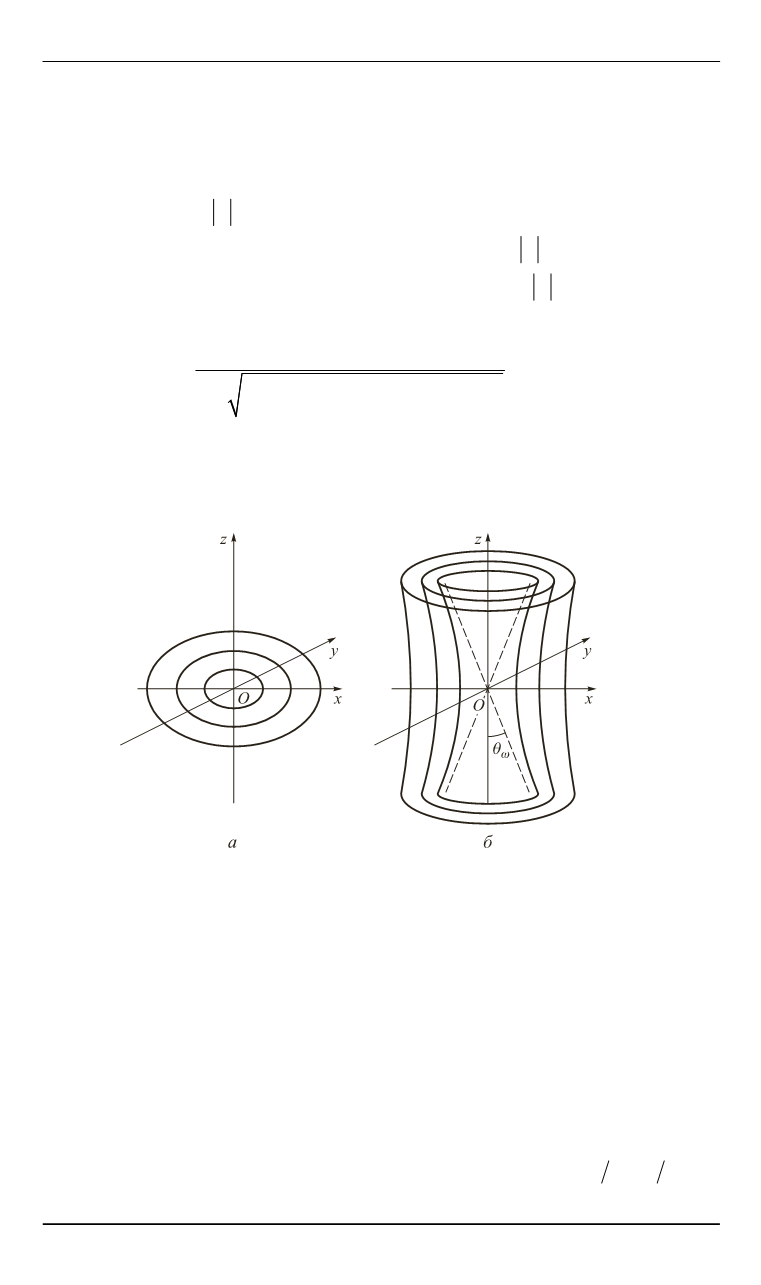
Рис. 3. Волновые фронты для акустической (
а
) и гравитационной (
б
)
ветвей акустико-гравитационных волн
Обсудим физический смысл величин
, ,
.
A
N N N
Частота
A
N
определяется произведением малого параметра
на большой параметр
.
c
Оценки показывают, что как для океана, так и для атмосферы частота
A
N
близка к частоте
N
Брента—Вяйсяля: для атмосферы
2 1
1, 9 10 c ,
N
2 1
2,1 10 c ,
A
N
для океана
2 1
~ 10 c ,
N
~
A
N
2 1
1,5 10 c
[2, 5, 9]. Из этих оценок следует, что при анализе диспер-
сии
( )
k
на частотах, близких к
,
N
необходимо учитывать сжимае-
мость среды. Отметим, что всегда
,
A
N N
2
2
2
2
A
N N c g c


