В.В. Булатов, Ю.В. Владимиров
22
2
2
0
2 4.
c
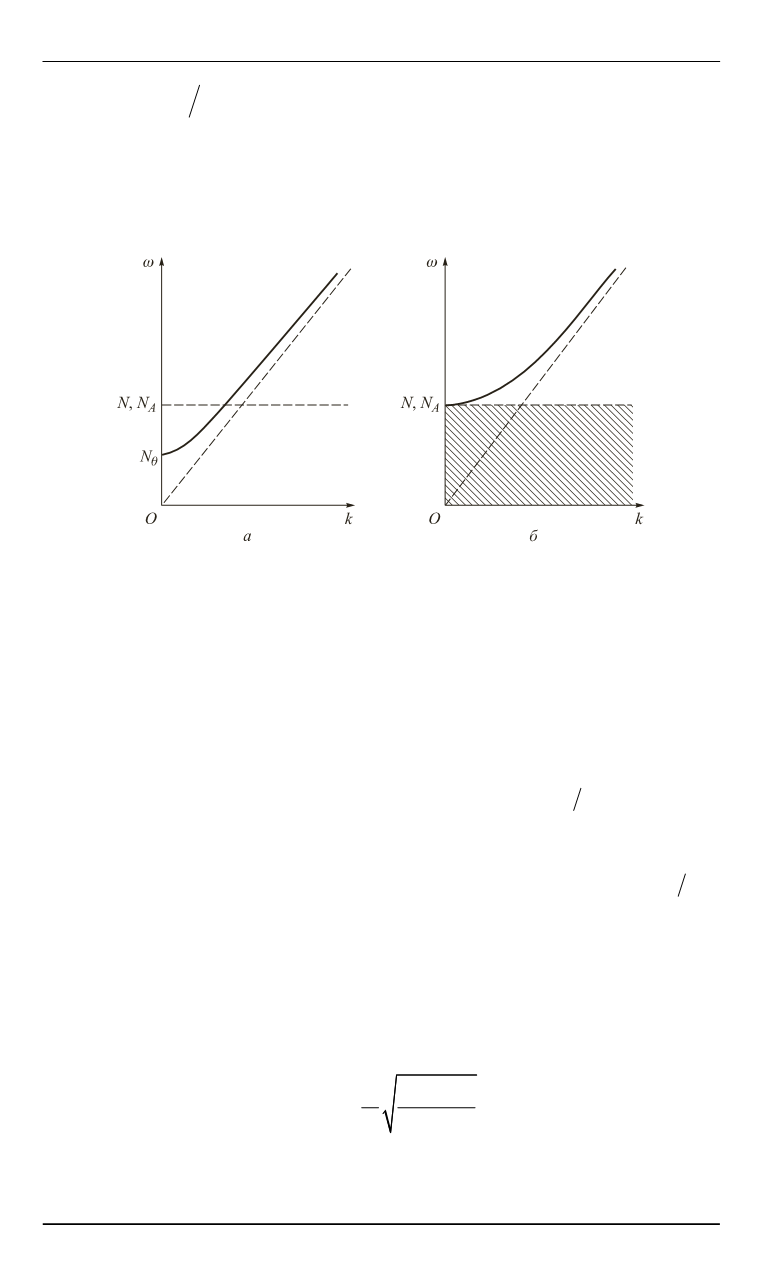
Таким образом, только при
0
2
отсутствует
верхний диапазон запирания и получается единая дисперсионная кривая
(рис. 4,
а
). При
0
частота Брента—Вяйсяля обращается в нуль и
пропадает нижняя ветвь дисперсионной кривой (рис. 4,
б
), в отличие от
предыдущего случая эта кривая не зависит от
.
Рис. 4. Дисперсионные кривые
( )
k
для
0
2
(
а
) и для
0
(
б
)
При рассмотрении низкочастотных внутренних гравитационных
волн в атмосфере обычно учитывают вращение Земли [3, 5, 9]. Одна-
ко это приводит к изменению лишь параметра
N
в уравнении (27):
2
2 2
2 2
sin
cos ,
z
N N
J
где
z
J
—
z
-компонента вектора угловой скорости вращения Земли.
Следовательно, вращение Земли заметно сказывается на поле
внутренних волн лишь при очень малых
3
10 рад .
z
J N
Влияние вращения Земли приводит к тому, что зависимость поля
акустико-гравитационных волн от
R
и
t
на горизонтальной плоско-
сти и вблизи нее такая же, как для поля на конусе с углом
,
z
J N
рассчитанном без учета вращения. Поэтому вращение Земли можно
учесть, например, изменив угловую зависимость
.
N
Обсудим теперь, как меняется вид дисперсионных кривых в
упомянутых выше упрощенных моделях. Сначала рассмотрим при-
ближение несжимаемой среды. В пределе
c
для
( )
k
получаем
выражение
2
2
2 2
( )
.
2
N
k
N
Очевидно, что при таком законе дисперсии пропадает акустиче-
ская ветвь дисперсионной кривой, а гравитационная ветвь с критиче-


