В.В. Булатов, Ю.В. Владимиров
20
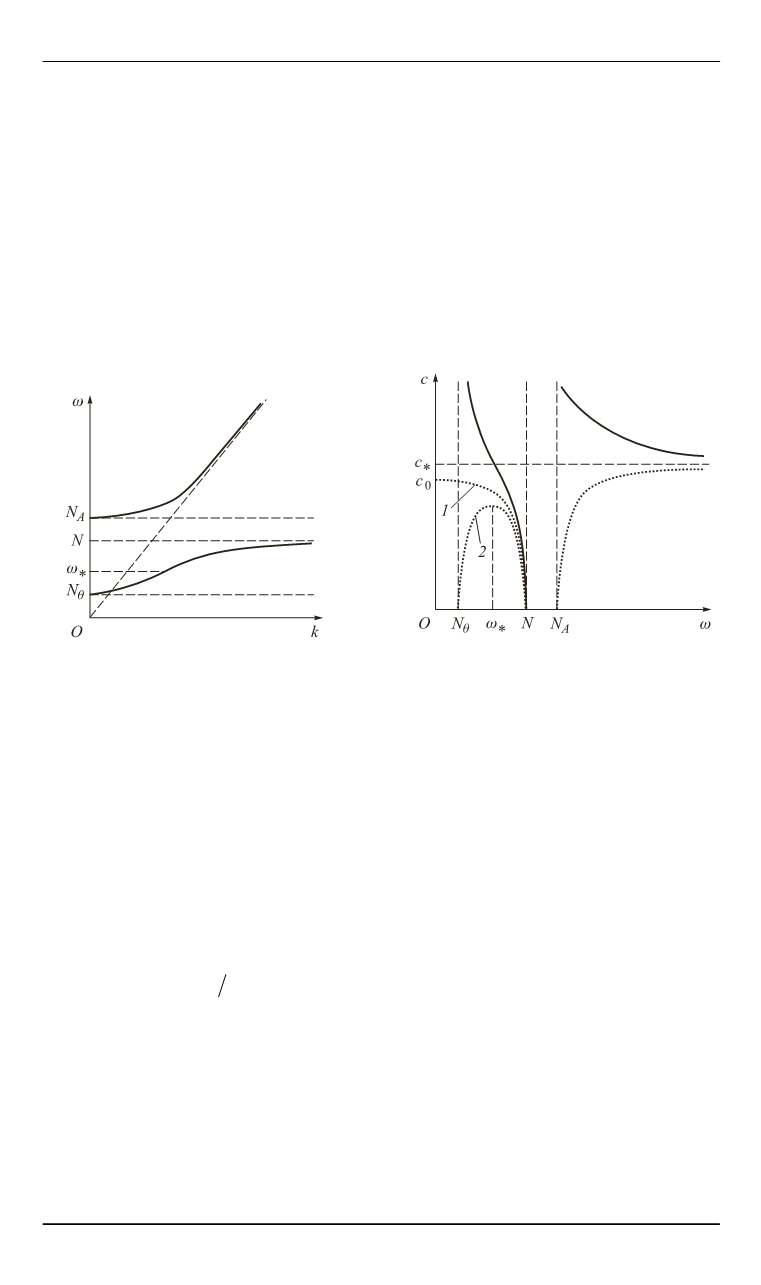
Дисперсионные кривые, показанные на рис. 2, имеют две ветви:
акустическую (при
>
N
A
) и гравитационную (при 0 <
<
N
). Фазо-
вые и групповые скорости (акустическая ветвь), стремятся к скорости
звука
c
при
.
C ростом
волны, описываемые акустической
ветвью, переходят в обычные звуковые. Нижней критической частотой
этих волн является
A
N
— наименьшая частота распространения аку-
стических волн. При частотах от
N
до
N
A
(верхний диапазон запира-
ния) волновое число
( )
k
чисто мнимое. В этом диапазоне нет рас-
пространяющихся плоских волн, а только экспоненциально затухаю-
щие при удалении от источника возмущений.
Кривые, изображенные на рис. 2, при 0 <
<
N
описывают грави-
тационную ветвь акустико-гравитационных волн. Верхняя критиче-
ская частота этой ветви равна
,
N
нижняя — зависит от угла
.
Если
волна распространяется строго горизонтально ( 0),
то нижняя
критическая частота отсутствует. Фазовая и групповая скорости го-
ризонтально распространяющейся волны при
0
стремятся к
значению
0
.
A
c Nc N c
Если
0,
то групповая скорость имеет
максимум на некоторой частоте ( ),
отличной от нуля.
Картины волновых фронтов поля, возбуждаемого гармоническим
источником, сильно различаются в случаях
A
N
и
N
(при
A
N N
поле синфазно и экспоненциально убывает при удалении
от источника). При
A
N
фронты имеют вид эллипсоидов враще-
ния (рис. 3,
а
), причем с ростом частоты их эксцентриситет убывает,
а в пределе при
они превращаются в сферы, как для обычных
Рис. 1. Дисперсионные кривые
( )
k
акустико-гравитационных
волн
Рис. 2. Фазовые (сплошные ли-
нии) и групповые (пунктирные
линии) скорости акустико-грави-
тационных волн при
= 0 (
1
) и
> 0 (
2
)


