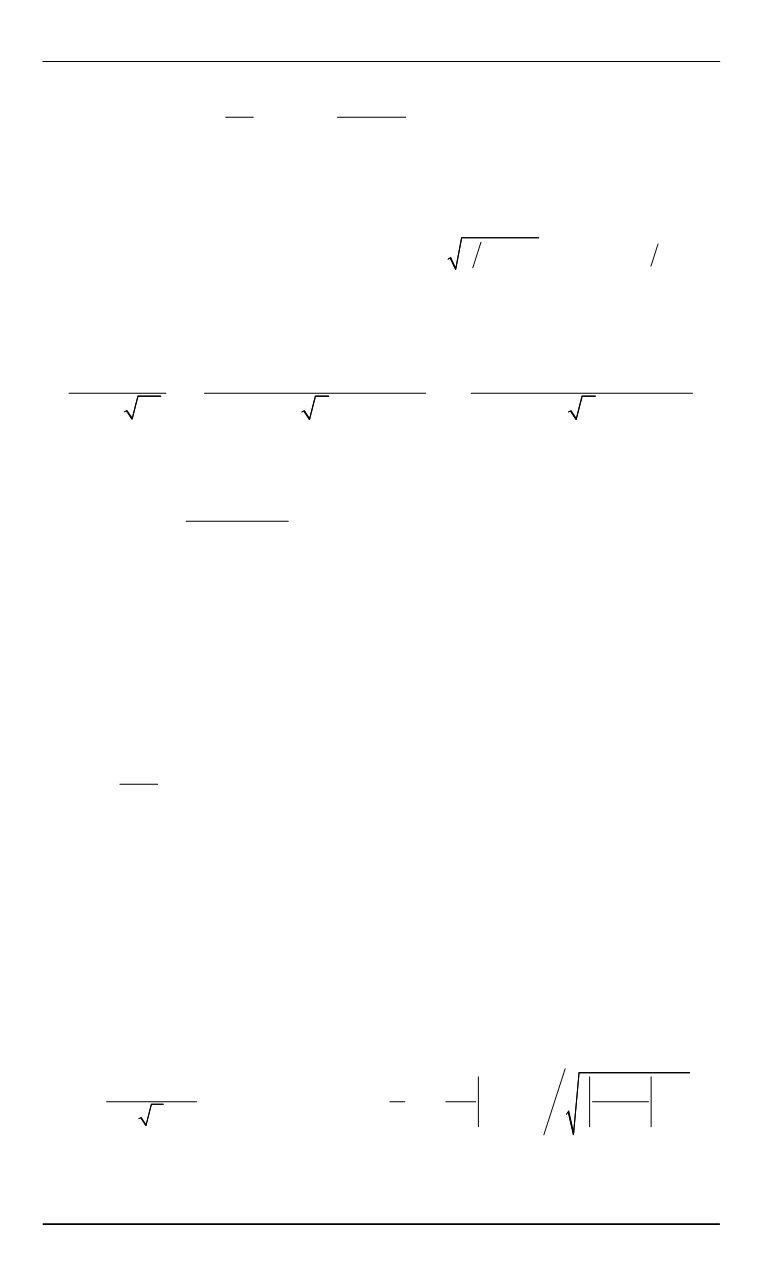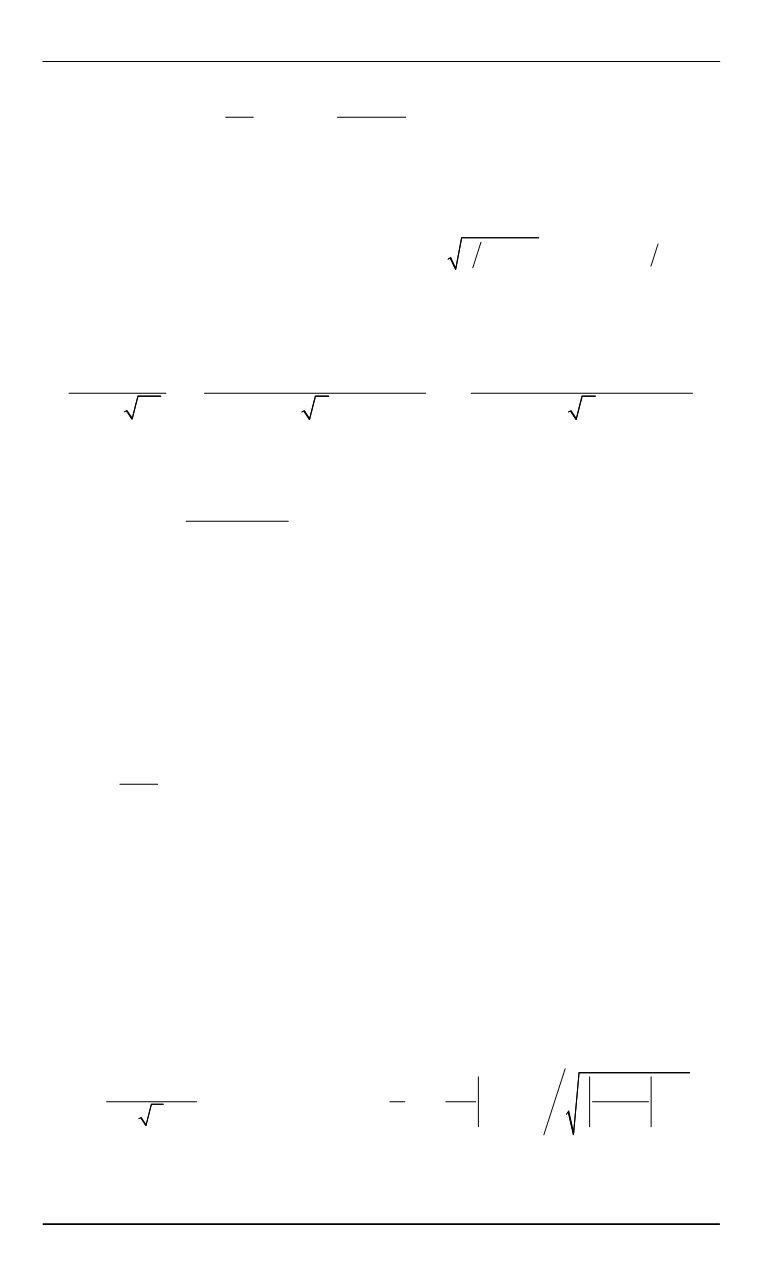
В.В. Булатов, Ю.В. Владимиров
12
2 2
0
0
0
0
( , , , )
( )
(
) ( , ) ( , ) .
4
( )
n
n
n
n
n
n
i
B
W r z z t
J k r
f
z k z k dk
k k
Поскольку рассматривается асимптотика
n
W
при больших
r
(дальнее поле), функцию Бесселя
0
( )
J k r
можно заменить на ее
асимптотику при
1,
k r
т. е.
0
( )
2
cos
4 .
J k r
k r
k r
В
результате имеем
2
2
3/2
exp (
) ( )
exp (
) ( )
exp( / 4)
.
4 2
n
n
n
W
i kr
t g k dk
i kr
t g k dk
i
r
k
k
(21)
Здесь
2
2
2
0
( )
( )
( , ) ( , )
( )
n
n
n
n
k f
g k
z k z k
k k
— четная функция по ,
k
а
функция
( )
n
k
продолжена в область
0
k
нечетным образом, точ-
ка ветвления
1/2
k
обходится в верхней полуплоскости.
Дисперсионная кривая функции
( )
n
k
есть монотонно возраста-
ющая функция по
.
k
Поэтому фазовая функция второго интеграла в
выражении (21) не имеет стационарных точек и этот интеграл при
,
,
t r
/
const
t r
экспоненциально мал.
Рассмотрим первый интеграл в формуле (21). Положим
( )
n
n
c k
k
— групповая скорость
n
-й волновой моды,
n
c
max ( ).
n
k
c k
Ясно, что при
n
r c t
первый интеграл также экспонен-
циально мал. При
n
r c t
можно применить обычный метод стацио-
нарной фазы. Обозначим через
( / )
j
j
r t
стационарные точки
первого интеграла, т. е. решения уравнения
/
( ).
n
r t c k
Вычисляя
при ,
,
t r
/ const
r t
асимптотику первого интеграла методом
стационарной фазы, получаем
0
( , , , )
exp( / 4)
( )
exp
( )
sign
,
4
4 2
j
j
n
n
n
j
n j
k
k
j
W z z r t
i
c
c k
i
r
t
T t
k
k
где