Дефокусировка нелинейных волновых пакетов на ледяном покрове - page 13

Дефокусировка нелинейных волновых пакетов на ледяном покрове
13
Будем рассматривать систему
уравнений (13) в окрестности крити-
ческого множества (17), определяемо-
го изменением только параметра
ˆ
    , 1   . Обозначим
ˆ( ),
   
 
( , ) ( , , ) ˆ , ˆ ˆ , b   w w      
где ˆ ˆ ˆ ( , , ).ˆb     Тогда система
уравнений (13) может быть преобра-
зована к виду (1).
Для понижения порядка системы
уравнений (13) используем теорему
о центральном многообразии (см.,
например, [31]). Для бесконечно-
мерных динамических систем эта
теорема справедлива при условии выполнения оценок убывания ре-
зольвенты оператора .  Справедливость этих оценок в настоящем
случае установлена в [31].
Разберем случай возникновения семейства уединенных волн, от-
ветвляющихся от состояния покоя для 1:1-резонанса, когда цен-
тральная часть спектра  состоит из пары ненулевых двукратных
мнимых собственных значений . iq  В этом случае размерность цен-
трального подпространства равна 4.
Собственные и присоединенные векторы оператора  при
iq    имеют вид
1 1
1
0 1
th
th th
; ; th 2 th
ch / ( ch ) sh / ( ch )
sh / ( ch ) ch / ( ch )
iq q q
q i iq q
iq q q q q
qy q q iy qy q q
i qy q q y qy q q
 

   
   
 
   
        
   
   
   
   
 
0 0 1 1 0 ; . iq iq          
Нелинейная вектор-функция ( , )w   (см. выражение (1)) при 0  
определяется так:
2 3 (0, ) ( , ) ( , , ) , N N    w w w w w w  
где точки обозначают члены высшего порядка,
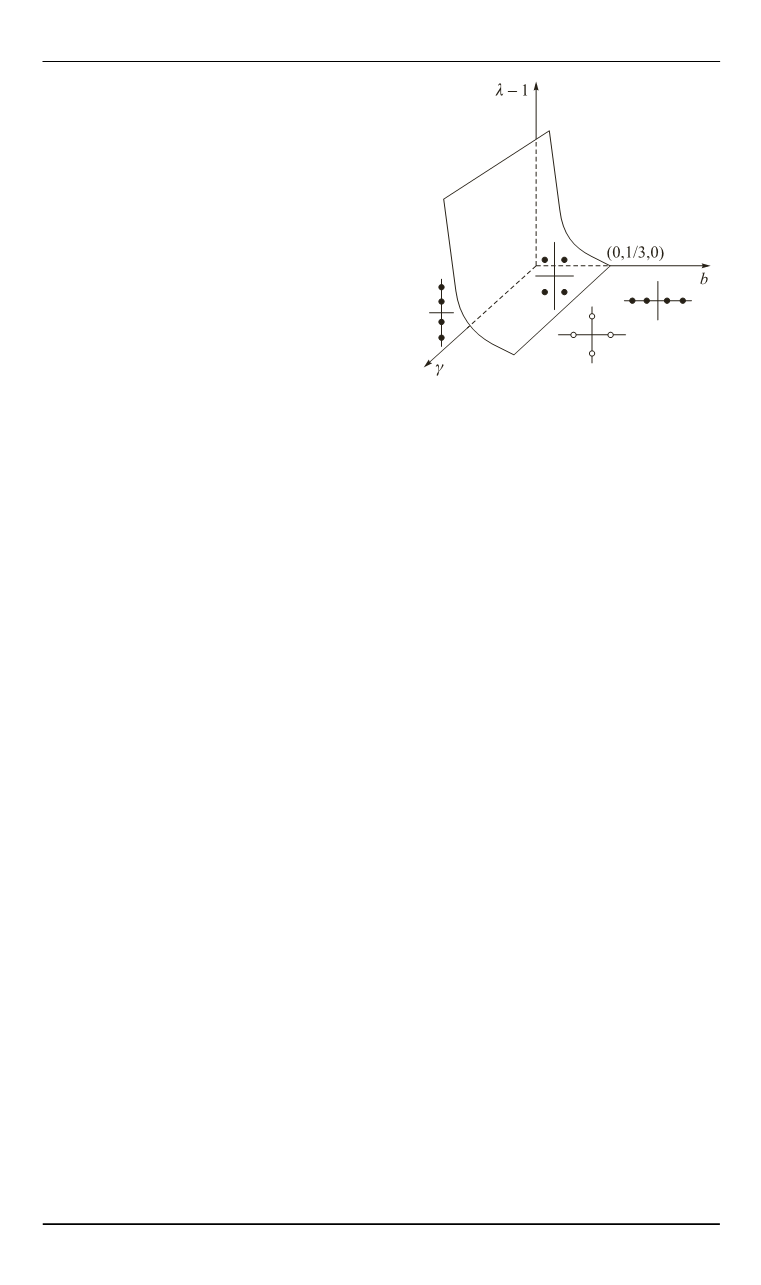
Рис. 2. Поверхности ˆ
1,    и
ˆ, b определяемые выражения-
ми, на которых происходит би-
фуркация в пространстве пара-
метров