Дефокусировка нелинейных волновых пакетов на ледяном покрове
17
т. е.
2
q
— кусочно-монотонная функция. Асимптотики для
2
q
будут
следующие:
при
ˆ 0
,
ˆ 0
b
2
2
2
8
19
3
,
0;
,
;
8
1
4
ˆ
8
5
q
q
q
q
q
при
ˆ 0
2
2
8
38475
11
,
0;
,
,
8
2
q
q
q
q
q
при
ˆ
b
= 0
2
2
4
171
79
,
0;
,
.
2
132
q
q
q
q
q
При
0
функция
2
q
меняет знак, что является типичным не
только при
0,
b
но также для любого фиксированного
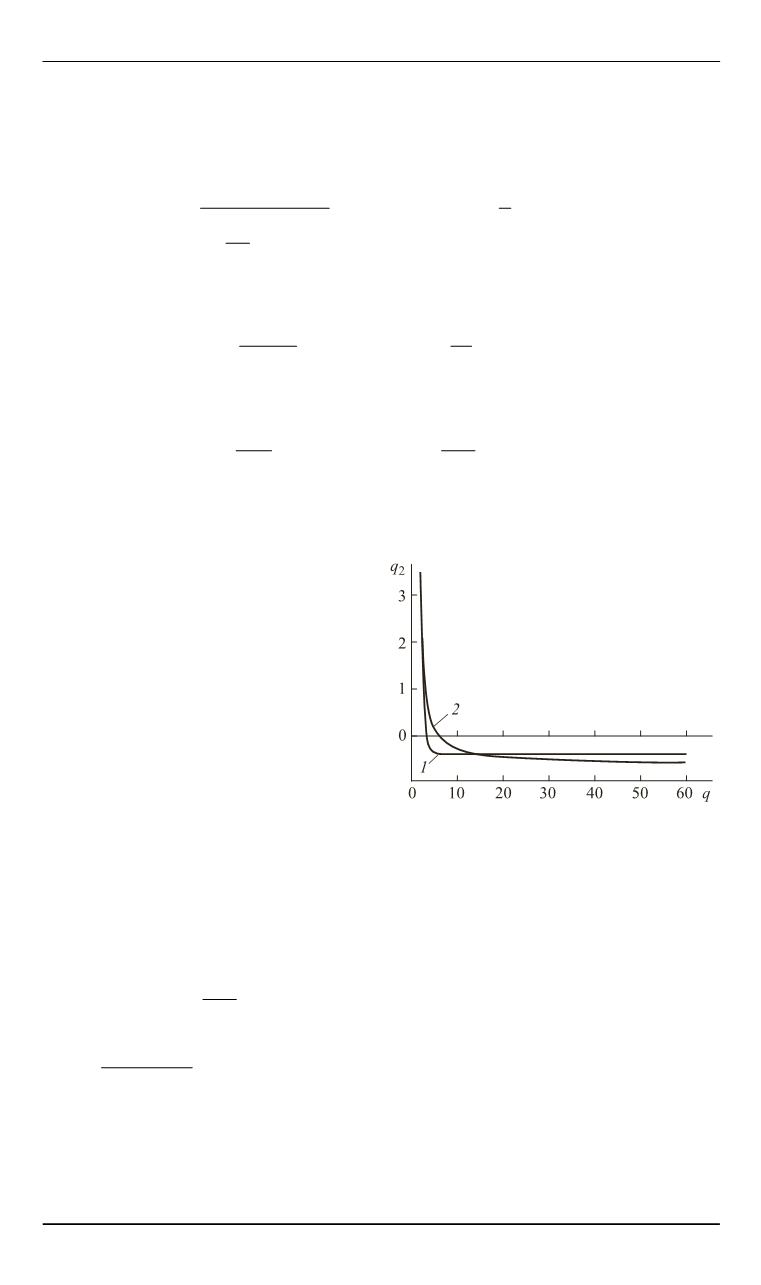
(рис. 3).
Поведение решений ради-
кально изменяется, когда
2
q
ме-
няет знак. Более того, в вырож-
денном случае (
2
q
лежит в малой
окрестности нуля) качественная
картина малых ограниченных
решений определяется коэффи-
циентом при членах следующего
порядка малости в разложении
полинома
Q
из (20) и отличается
от случая конечного
2
q
[43].
Пусть в уравнениях (20)
0
0
exp (
),
A
i qx
1
exp
B
1
(
).
i iqx
После указанной замены представим их в виде [37]
2
0
2
0
0 0
0
0
1 0
1
0 0 1
0
0 0
0 0
0
4
;
( , ,
)
(
)
(
)
( , ,
)
( , ,
)
,
du
u G u K H K
dx
d
K u u u Q u K G u K H
dx
(23)
где
2
0 0
;
u
2
1 1
.
u
Стационарные решения (23), а следовательно, и периодические
решения (20) определяются кратными корнями полинома
Рис. 3. Зависимость
q
2
(
q
) при
=
= 0,002 (
1
) и при
ˆ
0
b =
(
2
)


