Дефокусировка нелинейных волновых пакетов на ледяном покрове
21
ровка периодической волны. При
c
q q
вместо уединенных волно-
вых пакетов возникают темные солитоны и несущие периодические
волны, отвечающие волновым числам из этой области, являются
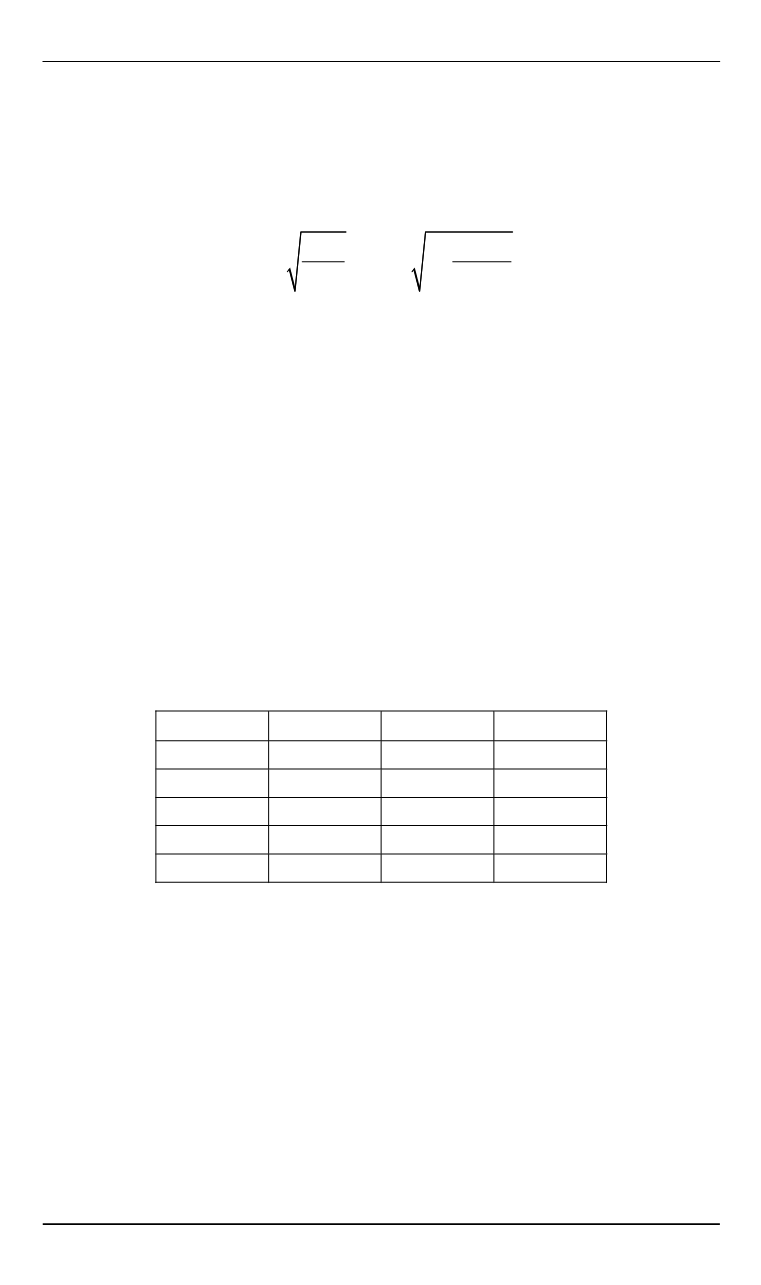
устойчивыми. Из определения безразмерных параметров
и
сле-
дует, что
3 8
4
3 3
,
,
J
J
H
V g
g
(27)
а из монотонности
ˆ
,
ˆ
— что глубина
H
возрастает с увеличением
.
q
Таким образом, при
c
H H
(где
c
H
— критическая глубина, со-
ответствующая
2
0)
q
волновое число
c
q q
и уединенные волно-
вые пакеты замещаются темными солитонами. Другими словами,
окрестность каждого резонансного волнового числа
q
становится
дефокусирующей. Критические значения
4, 34
c
и
0, 013
c
определяют подстановкой
c
q
в выражения (26). Резонансные волно-
вые числа
q
нормированы по глубине слоя жидкости
,
H
т. е.
,
q kH
где
k
— физическое волновое число. Критические значения
параметров
,
c
V
c
H
и
c
k
для некоторых толщин
h
ледяного покрова
приведены в таблице.
Значения критических параметров в зависимости
от толщины ледяного покрова
h
, м
V
c
, м/c
H
c
, м
k
c
, м/c
–1
0,01
2,23
2,15
2,69
0,1
5,28
12,12
0,48
0,4
8,88
34,28
0,17
0,8
11,52
57,65
0,1
1
12,53
68,14
0,085
Модуль Юнга
0
E
и коэффициент Пуассона
0
для льда равны
соответственно 5 000 МПа и 0, 35. Если при увеличении глубины
жидкости
H
число
q
переходит через
c
q
слева, то оно перестает
быть фокусирующим, а система не содержит семейство уединенных
волновых пакетов и уединенных волн огибающих с волновыми дли-
нами, близкими к
1
2 .
q
Заключение
. Таким образом, если фокусирующая область и су-
ществует где либо еще на дисперсионной кривой, она не содержит
волновых чисел, при которых групповая скорость равняется фазовой.
Из таблицы следует, что рассматриваемый эффект можно наблюдать
как для искусственных, так и для естественных бассейнов. Для тол-


