11
Математическое моделирование движения космического аппарата
Входной информацией этого алгоритма является точка, принад-
лежащая изолинии (φ
1,
i
, φ
2,
i
) и шаг поиска
h
φ
. Случай поиска второй
точки изолинии от случая поиска третьей и последующих точек отли-
чается выбором параметра
s
:
(
) (
)
2
2
1,
1, 1
2,
2, 1
, если 1;
,
g
i
i
i
i
h
i
h
s h
ϕ
ϕ
−
−
=
⎧
⎪
= ⎨
⎪ ϕ − ϕ + ϕ − ϕ
⎪⎩
если
i
> 1,
где (φ
1,
i
, φ
2,
i
), (φ
1,
i
– 1
, φ
2,
i
– 1
) — точки, принадлежащие изолинии,
h
g
= 1°.
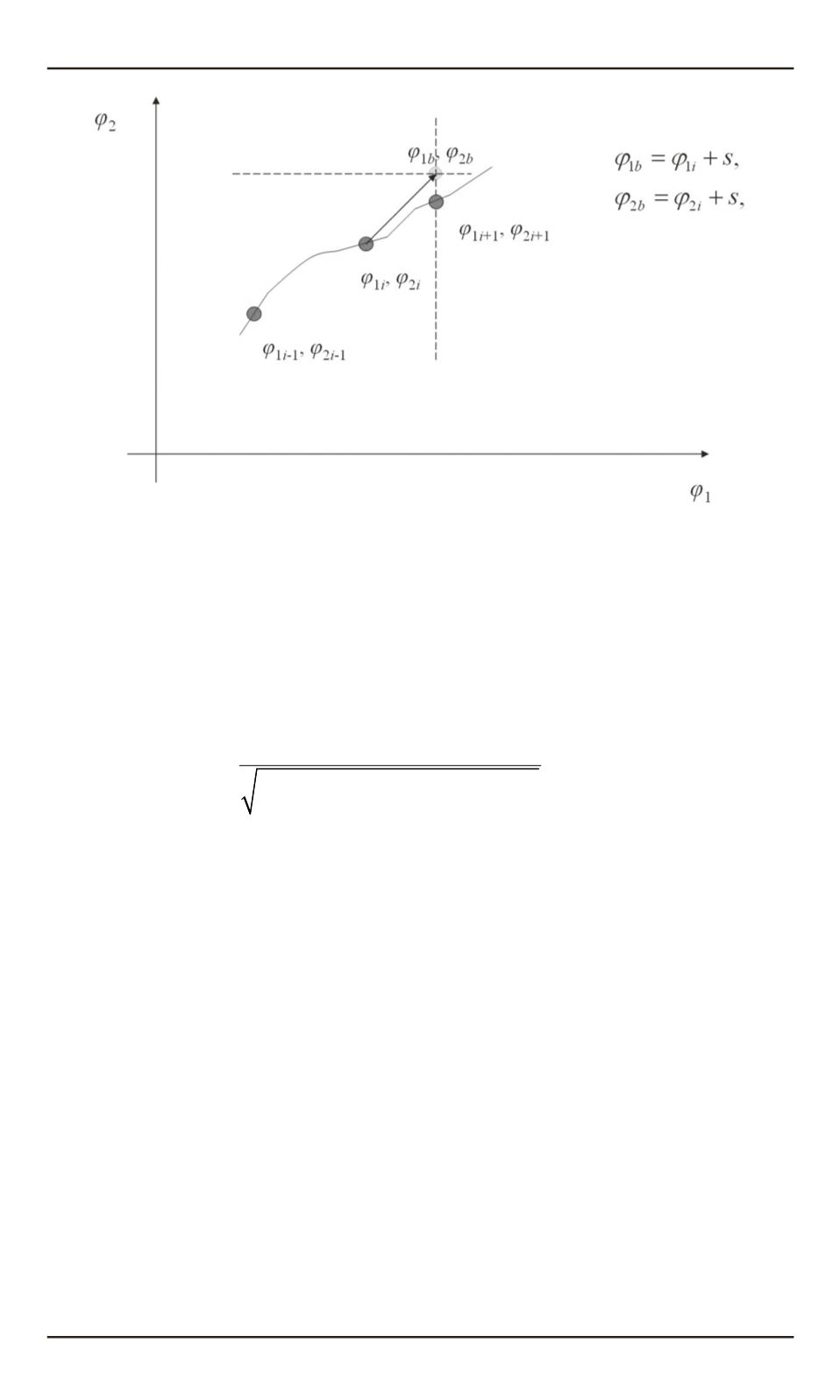
С использованием параметра
s
и последней известной точки изолинии
(φ
1,
i
, φ
2,
i
) устанавливается точка начала поиска (φ
1
b
, φ
2
b
) = (φ
1 +
s
, φ
2 +
s
)
и ищется пересечение изолинии с отрезком на плоскости φ1, φ2, соеди-
няющим точки (φ
1
b
–
jh
φ
, φ
2
b
) и (φ
1
b
+
jh
φ
, φ
2
b
) при
j
= 1, 2, …,
N
. Этот
отрезок проходит через точку начала поиска, параллелен оси φ
1
, а дли-
на его увеличивается с увеличением индекса
j
. Для этого ищется такое
значение
j
= 1, 2, …,
N
, при котором выполняется условие:
(
)
(
)
(
)
(
)
*
*
1
2
1
2
,
, ,
,
, ,
0.
b
b A B
b
b A B
f
jh
r f
jh
r
ϕ
π
ϕ
π
ϕ − ϕ θ θ −
ϕ + ϕ θ θ − ≤
(6)
Если значение
j
найдено, ищется такое значение φ
1
*
, чтобы точка
(φ
1
*
, φ
2
b
) принадлежала изолинии. Для этого используется алгоритм, ре-
ализующий метод бисекции.
Если значение индекса
j
, при котором выполняется условие (6), не
найдено, ищется точка пересечения изолинии с отрезком, который про-
Рис. 5.
Поиск точек изолинии


