7
Математическое моделирование движения космического аппарата
(
)
1
1
1
cos
,
t
t
A t
Ce De
λ
−λ
ξ =
ω + ϕ + +
(
)
(
)
2
2
1
1
1
sin
,
t
t
k A t
k Ce De
λ
−λ
ξ = −
ω + ϕ +
−
(1)
(
)
3
2
2
cos
.
B t
ξ =
ω + ϕ
где
(
)
2
1
1
1
рад
9 8
2 0,035384 ,
2
сут
L
L
L
n
B B B
ω =
− − + ≈
2
1
рад
0,034148 ,
сут
L
n B
ω =
≈
(
)
2
1
1
рад
9 8
2 0,042734 ,
2
сут
L
L
L
n
B B B
λ =
− + − ≈
(
)
2
1
1
1
1
2 1 0,54525,
2 /
L
k
B
n n
⎡
⎤
⎛ ⎞λ
⎢
⎥
=
− − ≈ −
⎜ ⎟
λ ⎢
⎥
⎝ ⎠ ⎣
⎦
(
)
2
1
2
1 1
1
1
2 1 3,1873,
2 /
L
k
B
n n
⎡
⎤
⎛ ⎞ω
⎢
⎥
=
+ + ≈
⎜ ⎟
ω ⎢
⎥
⎝ ⎠ ⎣
⎦
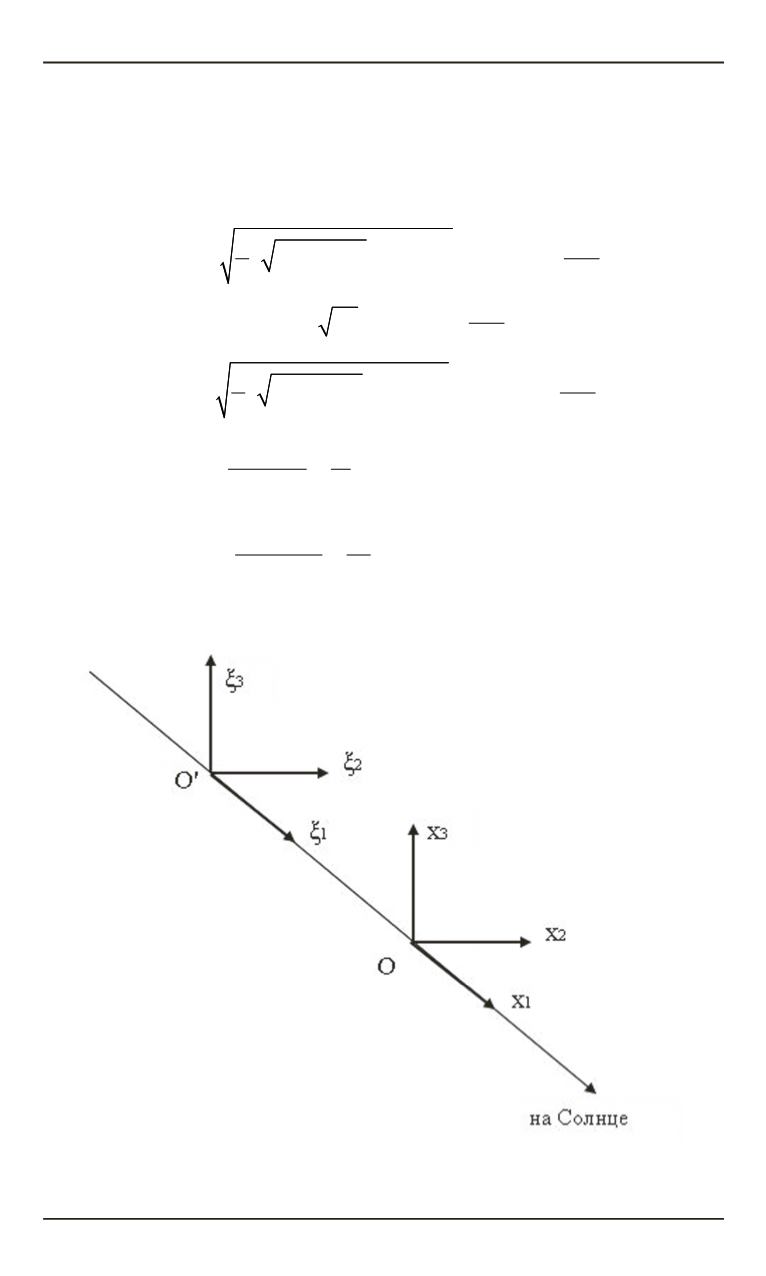
Рис. 3.
Системы координат
Ox
1
x
2
x
3
и
O
′ξ
1
ξ
2
ξ
3


