15
Математическое моделирование движения космического аппарата
Далее для вычисления элементов орбиты, и в том числе расстояния
перицентра
r
π
по вектору
1 2 3 1 2 3
( , , , , , )
x x x x x x
траектория перелета раз-
бивается на три участка:
• от Земли до входа в сферу действия Луны;
• полет в сфере действия Луны;
• полет после выхода из сферы действия Луны до входа в окрест-
ность
L
2
.
Для определения момента выхода из сферы действия Луны следу-
ет использовать численное интегрирование. При этом расчет вектора
состояния КА целесообразно выполнять до достижения расстояния
50 тыс. км от центра Земли. Далее вычисляются оскулирующие эле-
менты орбиты, по ним рассчитывается расстояние перицентра.
Основными параметрами, характеризующими гравитационный ма-
невр у Луны, являются Δ
GAM
— модуль импульса, сообщаемого КА
в результате гравитационного маневра, и P
GAM
— модуль проекции им-
пульса гравитационного маневра на направление скорости КА. Если
P
GAM
> 0, импульс гравитационного маневра направлен на разгон КА,
иначе ― на торможение.
Параметры Δ
GAM
и P
GAM
вычисляются по следующим формулам:
(
)
GAM
GAM
,
,
,
out
in out
out
in
out
−
Δ = − Ρ =
v v v
v v
v
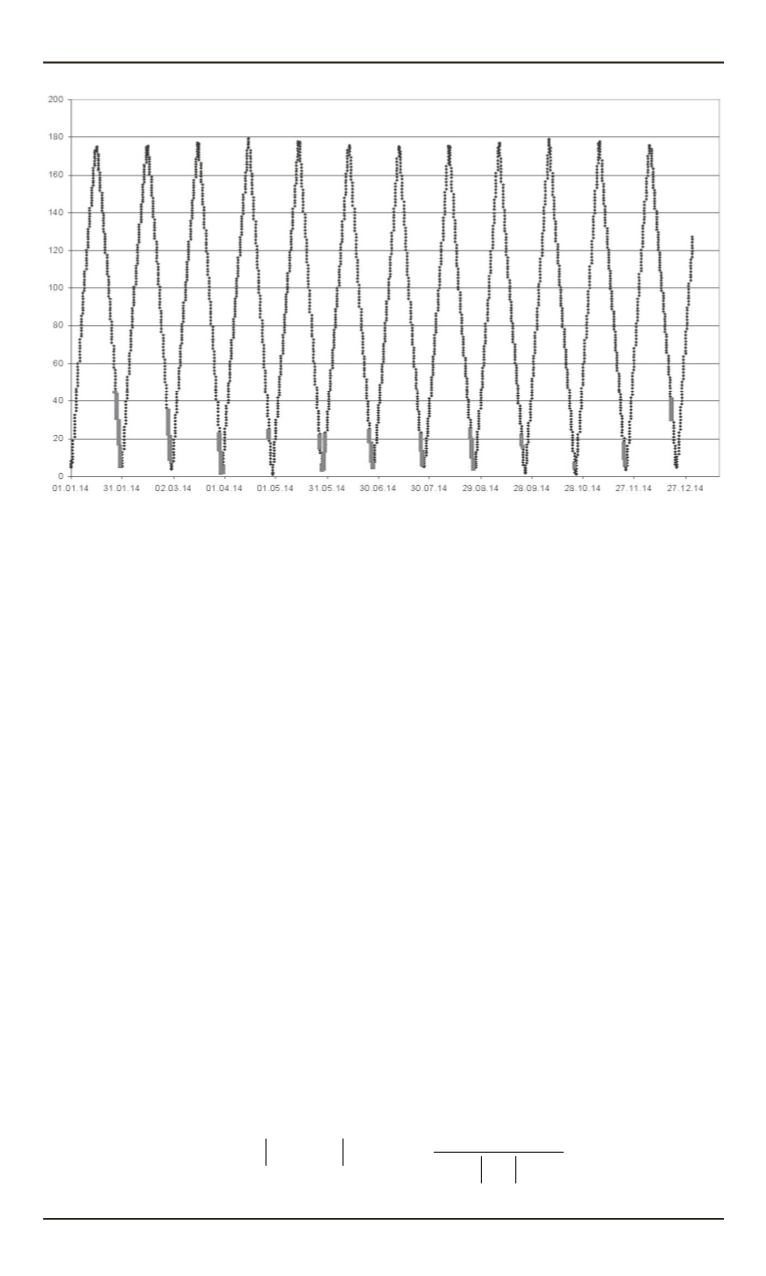
Рис. 7.
Угол между направлениями от Земли на Солнце и Луну


