2
Г.К. Боровин, И.С. Ильин, Г.С. Заславский, С.М. Лавренов, В.В. Сазонов и др.
Гало-орбита задается четырьмя параметрами:
А
— удаление КА от
точки
L
2
в плоскости эклиптики;
В
— удаление КА от точки
L
2
в пло-
скости, ортогональной эклиптике; φ
1
— фаза колебательного движе-
ния КА в проекции на плоскость эклиптики; φ
2
— фаза колебательного
движения КА в проекции на плоскость, ортогональную эклиптике.
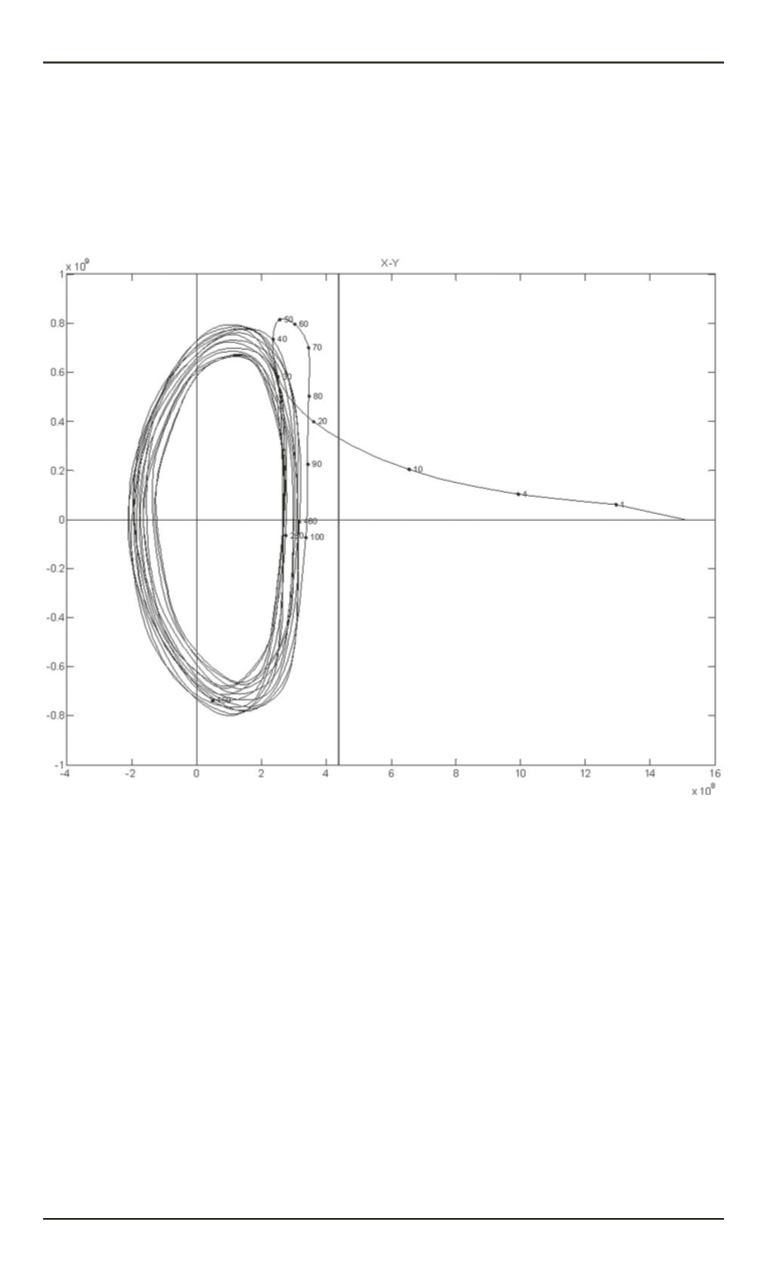
Пример траектории перелета и полета по гало-орбите показан на
рис. 1, где представлена проекция траектории на плоскость
OXY
вра-
щающейся СК с началом в точке
L
2
. Ось
OX
направлена от точки
L
2
к Земле. Ось
OZ
ортогональна плоскости эклиптики. Ось
OY
дополняет
систему до правой. Цифры, указанные вдоль кривой, — сутки полета.
Примерно через 20 сут полета КА выходит из сферы действия Земли,
а через 100 сут переходит на гало-орбиту. Траектория полета по гало-
орбите приведена с учетом выполнения коррекций удержания. При по-
лете по гало-орбите КА облетает точку
L
2
за 180 сут.
Статья содержит четыре раздела. В первом разделе описан метод
построения начального приближения для перелета с низкой орбиты
Рис. 1.
Перелет без использования гравитационного маневра у Луны: траек-
тория перелета и проекция гало-орбиты вокруг точки
L
2
на плоскость
OXY
вращающейся СК


