Разработка и исследование алгоритмического обеспечения …
13
S
B
M
B
ε
0
S
B
От БИНС
Угловая
погрешность
Β
ω
ˆ
Начальные
условия
Модель
ВИУС
Алгоритмы ориентации
БИНС
Эталонная ориентация
Β
ω
Рис. 10.
Блок-схема оценки точности алгоритмов ориентации
Практика показывает, что вращение БИНС с некоторой фиксиро-
ванной угловой скоростью приводит к существенному ухудшению
точности в течение достаточно короткого промежутка времени. При-
чина этого заключается в существовании погрешностей по масштаб-
ному коэффициенту ВИУС (это может быть показано и теоретиче-
ски), а также, предположительно, и погрешностями процедур инте-
грирования. Вторая причина представляет больший интерес. Поэтому
далее при моделировании входная угловая скорость для оценки точ-
ности принимается константой, т. е.
ω
B
= const
.
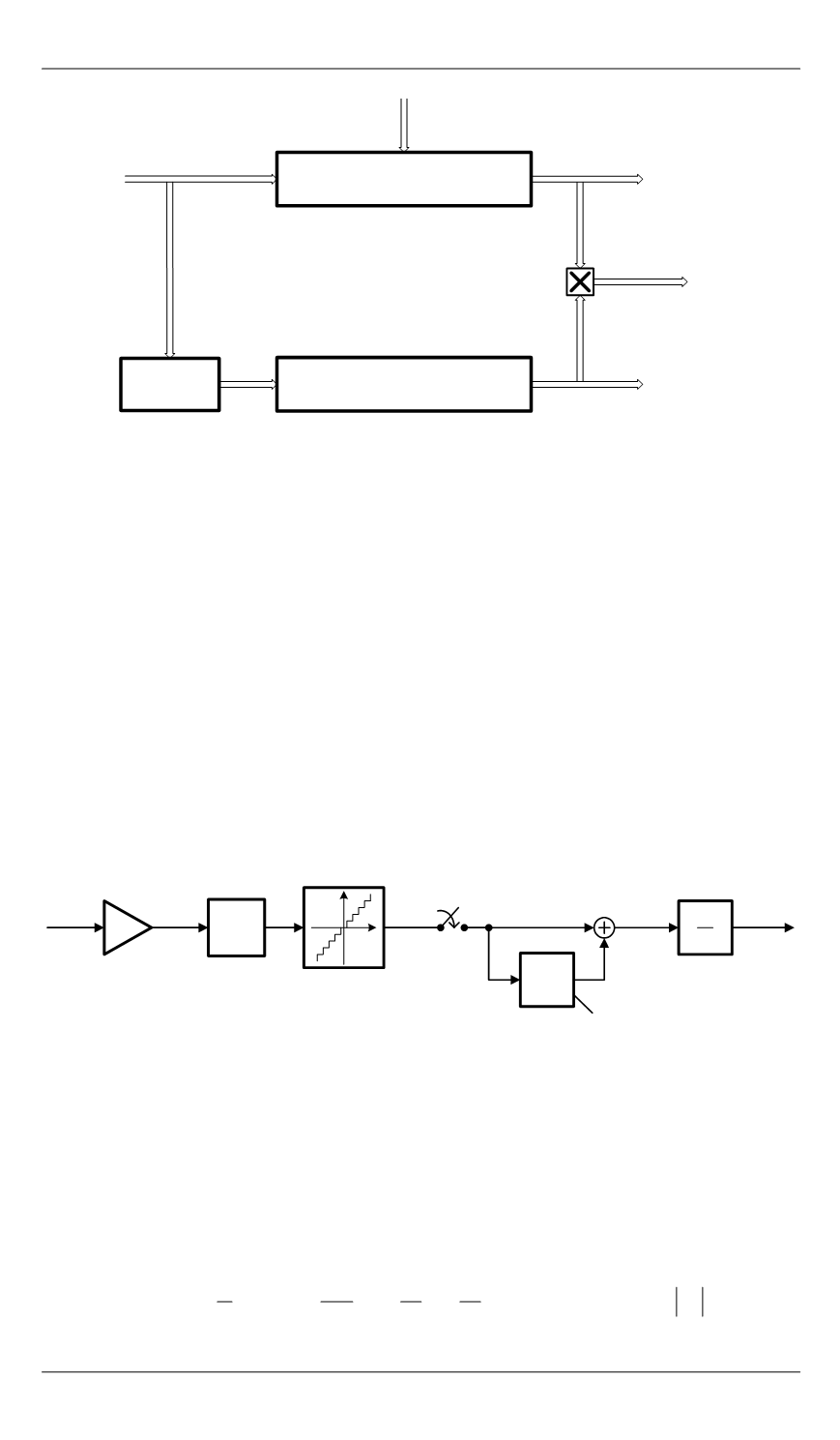
Принятая модель ВИУС соответствует блок-схеме на рис. 11. Здесь
ω(
t
)
— измеряемая угловая скорость;
θ(
t
)
— кажущийся угол;
k
=
=
k
0
— параметр ВИУС.
Entier
z
-1
Δ
t
N
[имп]
θ
(
t
)
[рад]
-
] рад [
)(ˆ
t
θ
∇
Элемент задержки
на такт
ω
(
t
)
[с
-1
]
Δ
N
[имп]
k
∫
0
1
k
Рис. 11.
Модель ВИУС
Рассмотрим алгоритмы ориентации, реализуемые в БИНС.
Использование многошагового метода для интегрирования
уравнений углового движения БИНС.
Если выбрать вектор истин-
ного поворота
Φ
(
t
) в качестве основы, то соответствующее кинема-
тическое уравнение углового движения имеет вид
(
)
2
1
1 Φ Φ
1 ctg
, Φ
2
Φ 2 2
⎛
⎞
= ω + × ω + −
× × ω =
⎜
⎟
⎝
⎠
Φ Φ
Φ Φ
Φ
,


