Е.С. Лобусов, А.В. Фомичев
6
u
∫
A
Алгоритмы БИНС
С
( )
[
]
[
]
.
1
1-
1-
1
1
1
~
~ ~
~
;
;
−
−
−
Δ
−
Δ
⎥
⎦
⎤
⎢
⎣
⎡
+⎟
⎠
⎞ ⎜
⎝
⎛ ′
′
+
′
+
′
=
=
=
=
i
i i
i
i i
Ф
i
i
i
i i i
i i
Ф
i
i
i
i i
i
СRС P PСK-I P
R СССP K
Q A PA P
P
Ф
K
w
x
δ
u
δ
y
δ
y
B
ˆ
v
δ
⎟
⎠
⎞
⎜
⎝
⎛
+ −
ν
ЗД
B
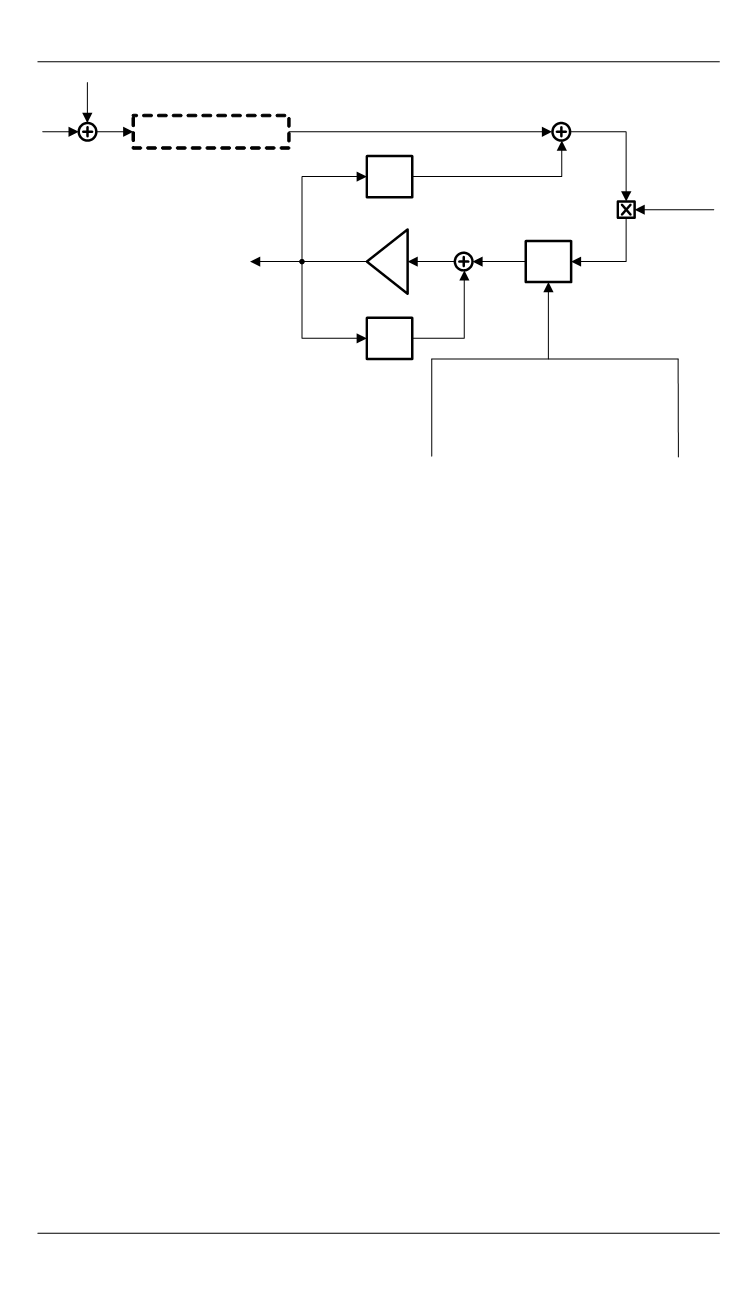
Рис. 5.
Фильтр Калмана в составе корректирующего контура
При определении процедуры вычисления оптимального коэффи-
циента фильтра Калмана предполагается, что случайные воздействия
на систему имеют следующие статистические свойства [5, 10].
Вектор случайных внешних воздействий
w
i
размерностью (
n
×
1) —
гауссов дискретный белый шум с нулевым средним
{ }
0,
i
i
= ∀
M w
.
Матричная корреляционная функция для этого шума имеет вид
{ }
T
κ
(
)
i j
i
i j
=
−
δ
M w w Q
,
где
δ
κ
— функция Кронекера, принимающая следующие значения:
κ
0 при ,
(
)
1при .
i j
i j
i j
≠
⎧
= − = ⎨
=
⎩
δ
Q
i
— симметрическая, неотрицательно определенная, изменяющаяся
во времени корреляционная матрица, размерностью (
n
×
n
). Поскольку
данная матрица — неотрицательно определенная, то допускается, что
w
i
= 0.
Вектор измерительного шума
v
i
размерностью (
r
×
1) — гауссов
дискретный белый шум с нулевым средним
{ }
0,
i
i
= ∀
M v
.
Матричная корреляционная функция для этого шума имеет вид
{ }
T
κ
(
)
i j
i
i j
=
−
δ
M v v R
,
где
R
i
— симметрическая, положительно определенная, изменяюща-
яся во времени корреляционная матрица, размерностью (
r
×
r
).


