Разработка и исследование алгоритмического обеспечения …
7
Измерительный шум
v
i
считается некоррелируемым с шумовой
помехой
w
k
, а также с вектором начального состояния системы, т. е.
{
}
T
0,
,
k j
k j
= ∀
v
M w
и
{ }
T
0
0,
k
k
= ∀
M v x
.
Выражения для нахождения параметров фильтра Калмана непо-
средственно показаны на рис. 5.
Однако структуру фильтра Калмана, показанную на рис. 5, мож-
но изменить и получить полное соответствие со структурой, приве-
денной на рис. 3. Отличие заключается в том, что в новой схеме (см.
рис. 6) нет возможности определить угловую погрешность.
u
Алгоритмы БИНС
( )
[
]
[
]
.
1
1-
1-
1
1
1
~
~ ~
~
;
;
−
−
−
Δ
−
Δ
⎥
⎦
⎤
⎢
⎣
⎡
+⎟
⎠
⎞ ⎜
⎝
⎛ ′
′
+
′
+
′
=
=
=
=
i
i i
i
i i
Ф
i
i
i
i i i
i i
Ф
i
i
i
i i
i
СRС P PСK-I P
R СССP K
Q A PA P
P
Ф
K
w
u
δ
B
ˆ
v
δ
⎟
⎠
⎞
⎜
⎝
⎛
+ −
ν
ЗД
B
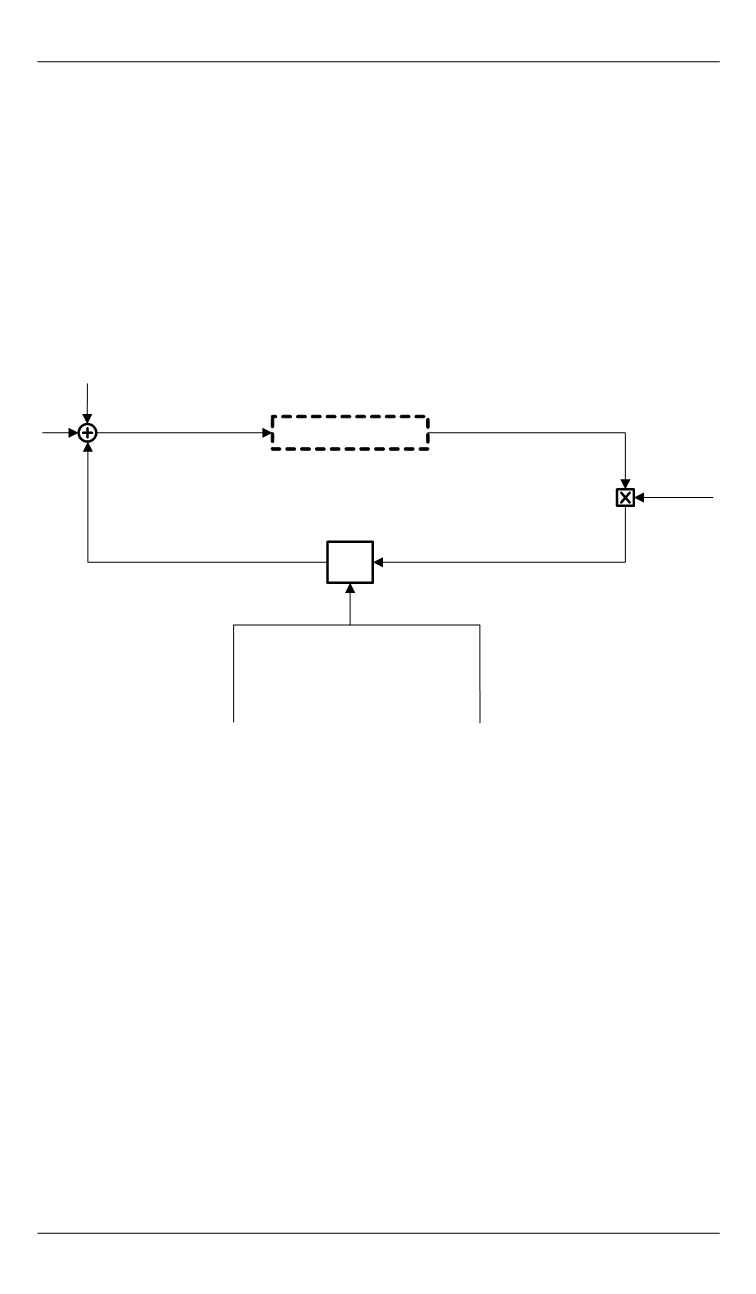
Рис. 6.
Фильтр Калмана в составе корректирующего контура
Недостаток подхода с использованием фильтра Калмана связан с
незнанием статистических характеристик собственных погрешностей
ВИУС и неопределенностью задания уровня шума измерения для
данных от ЗД. Поэтому в данном случае оказывается целесообразнее
использовать подходы классической теории регулирования и алгебру
кватернионов [3].
Угловая ошибка оценивается векторной частью кватерниона рас-
согласования
δ
B
γ
γ
ˆ
δ
=
B B B
.
В [3] показано, как обеспечить асимптотическую устойчивость
контура коррекции выбором определенного закона регулирования.
В простейшем виде коэффициент закона регулирования
K
= [
k
1
,
k
2
,
k
3
]
T
соответствует векторной константе, выбираемой из
условия получения определенного качества переходного процесса в


