Е.С. Лобусов, А.В. Фомичев
8
контуре коррекции. В этом случае устранение рассогласования про-
исходит по кратчайшему угловому расстоянию.
Корректируемый алгоритм навигации
позволяет повысить
точность расчета навигационных переменных вектора линейной ско-
рости и радиуса-вектора положения МКА в ИСК.
Уравнение навигации записывается в геоцентрической экватори-
альной системе координат
( )
γ
γ
γ γ
a
a
= +
v a g r
,
(1)
где
γ
a
v
— вектор абсолютной линейной скорости в ИСК;
a
γ
— вектор
кажущегося ускорения в ИСК;
γ
a
r
— радиус-вектор в ИСК;
( )
γ γ
a
g r
—
вектор гравитационного ускорения.
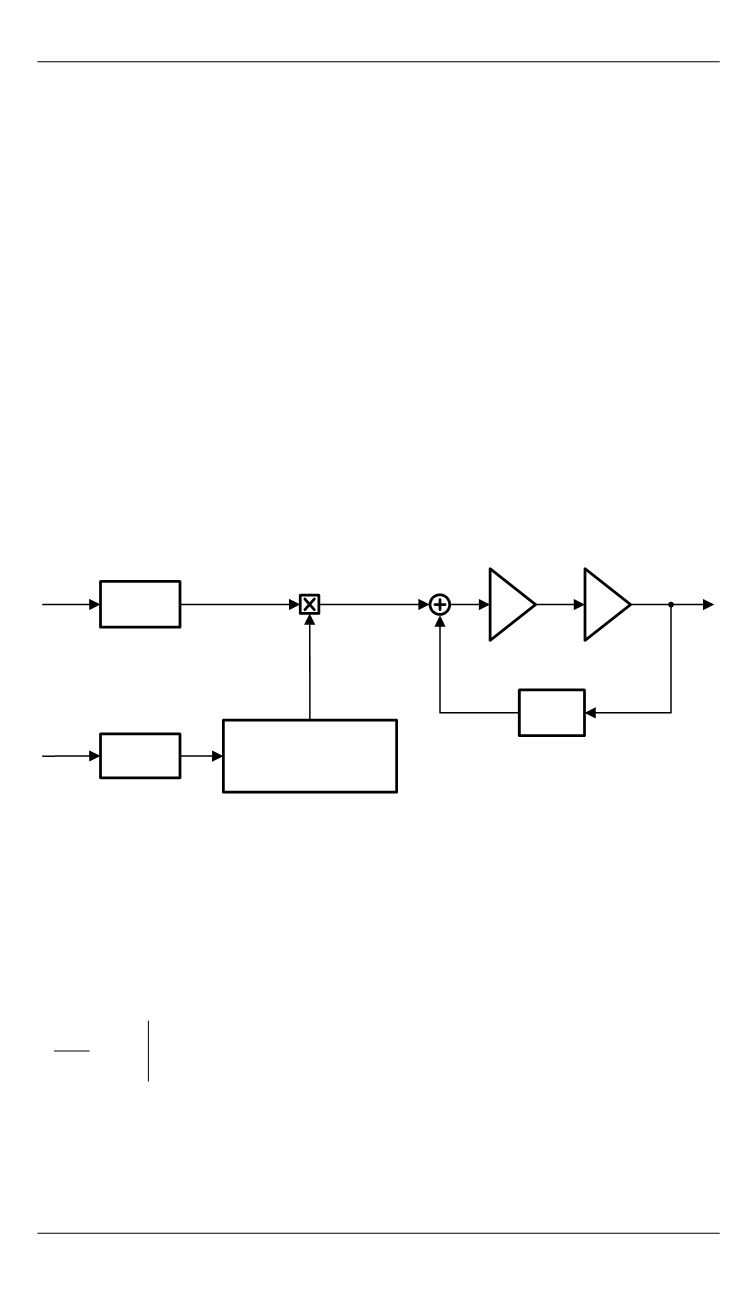
Общая блок-схема БИНС в ИСК приведена на рис. 7 (см. также
блок-схему на рис. 1), где символом ˆ определяются оценки перемен-
ных; ВИУС — векторный измеритель угловой скорости; ВИЛУ —
векторный измеритель линейных ускорений.
B
a
B
a
ω
γ
B
ˆ
ВИЛУ
ВИУС
γ
a
v
ˆ
γ
a
r
ˆ
Кинематические
уравнения
углового движения
∫
∫
B
a
ˆ
γ
a
ˆ
B
a
ω
ˆ
( )
γ
a
rg
Рис. 7.
Блок-схема БИНС в ИСК
К уравнению (1) добавляется и дифференциальное уравнение для
радиуса-вектора
a
a
γ
γ
=
r v
.
(2)
Начальные условия по вектору состояния уравнения (1)
T
0
,
t
d
dt
γ
γ
=
⎡
⎤
⎢
⎥
⎣
⎦
r
r
задаются для звездного времени.
Кинематические уравнения углового движения, записанные с по-
мощью кватернионов, имеют вид
ˆ
2
ω
a
γ
γ
=
B
B B
или
ˆ
2
a
γ
γ
γ
γ
= − ω
B
B B B B
,
(3)


