10
Н.И. Сидняев, Ю.С. Ильина, Д.А. Крылов
2, 1
2
2,
.
1
n
n
u hg
u
h
После совершения шагов 1 и 2
получаем решение для
t
= ∆
t
. Для
получения решения при
t
= 2∆
t
(вторая строка снизу на рис. 6) по-
вторяем шаги 1 и 2, поднявшись на
одну строку вверх, т. е. увеличив
i
на 1 и используя
u
i
,
j
с предыдущей
строки. Аналогично вычисляется
решение и в последующие момен-
ты времени
t
= 3∆
t
, 4∆
t
, …
Замечания.
1. У явной схемы
есть серьезный недостаток. Если
шаг по времени оказывается доста-
точно большим по сравнению с ша-
гом по
x
, погрешности округления
могут стать настолько большими,
что полученное решение потеряет
смысл. Отношение шагов по
t
и
x
зависит от уравнения и граничных
условий, но в общем случае шаг по
времени должен быть много мень-
ше шага по координате. Доказано,
что для применимости явной схемы
должно выполняться условие
k
/
h
2
0,5.
2. Справедливо следующее эмпирическое правило: если уменьшать
шаги ∆
t
и ∆
x
, то погрешность аппроксимации частных производных
конечными разностями тоже будет уменьшаться, однако чем мельче
сетка, тем больше вычислений необходимо совершить и, следовательно,
тем больше будут погрешности округления.
3. Для гиперболической задачи
Уравнение в частных производных (УЧП)
Граничные условия (ГУ)
Начальные условия (НУ)
1
2
, 0 1, 0
,
(0, )
( ),
0
,
(1, )
( ),
( , 0) ( ),
( , 0)
( ), 0 1,
tt
xx
t
u u
x
t
u t
g t
t
u t
g t
u x
x
u x
x
x
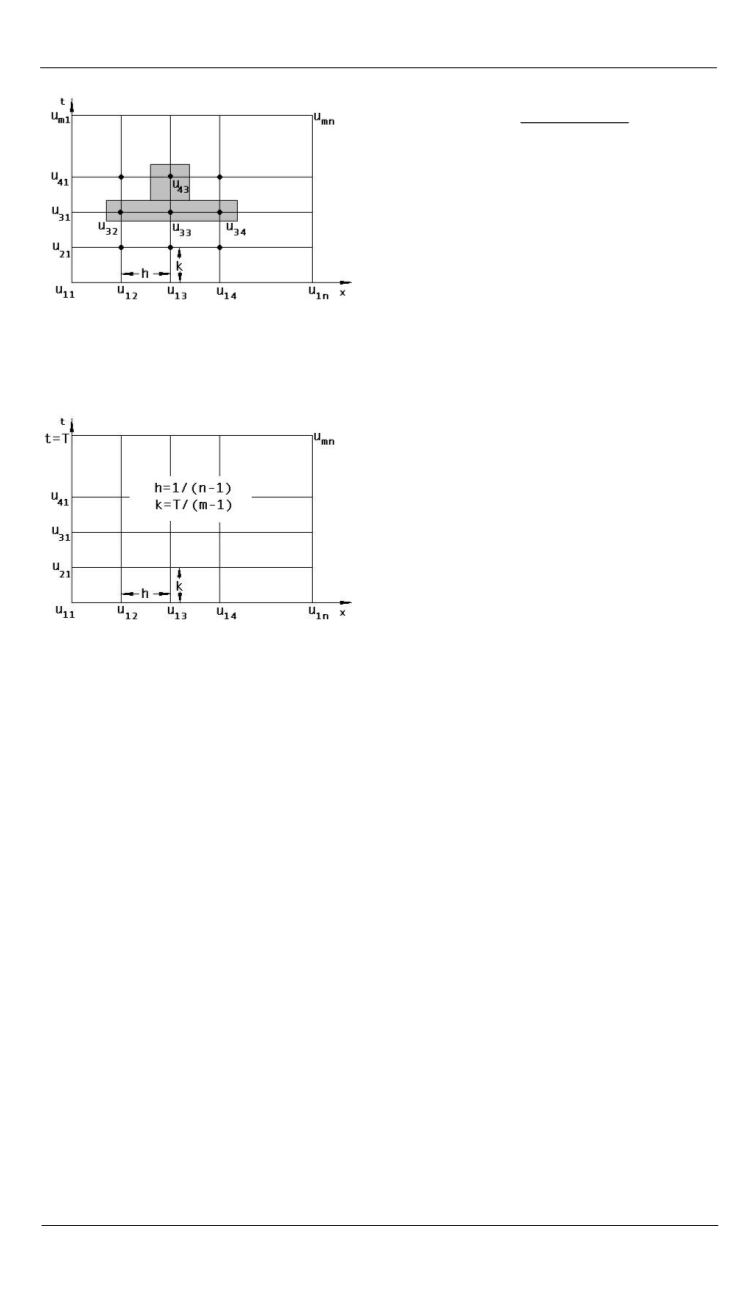
Рис. 6.
Иллюстрация явной разност-
ной схемы:
n
— число узлов сетки вдоль оси
x
;
m
— число узлов сетки вдоль оси
y
;
h
= 1/(
n
– 1),
k
=
T
/(
m
– 1)
Рис. 5.
Сетка для уравнения тепло-
проводности


