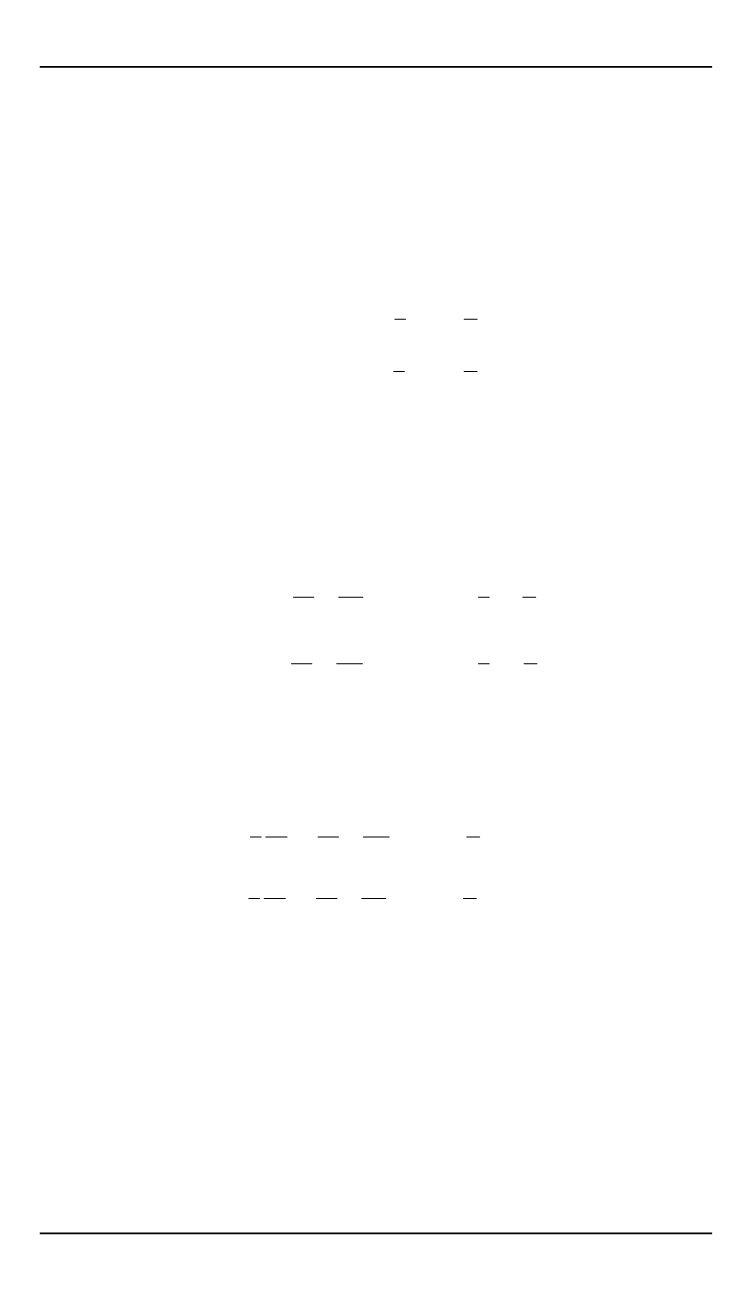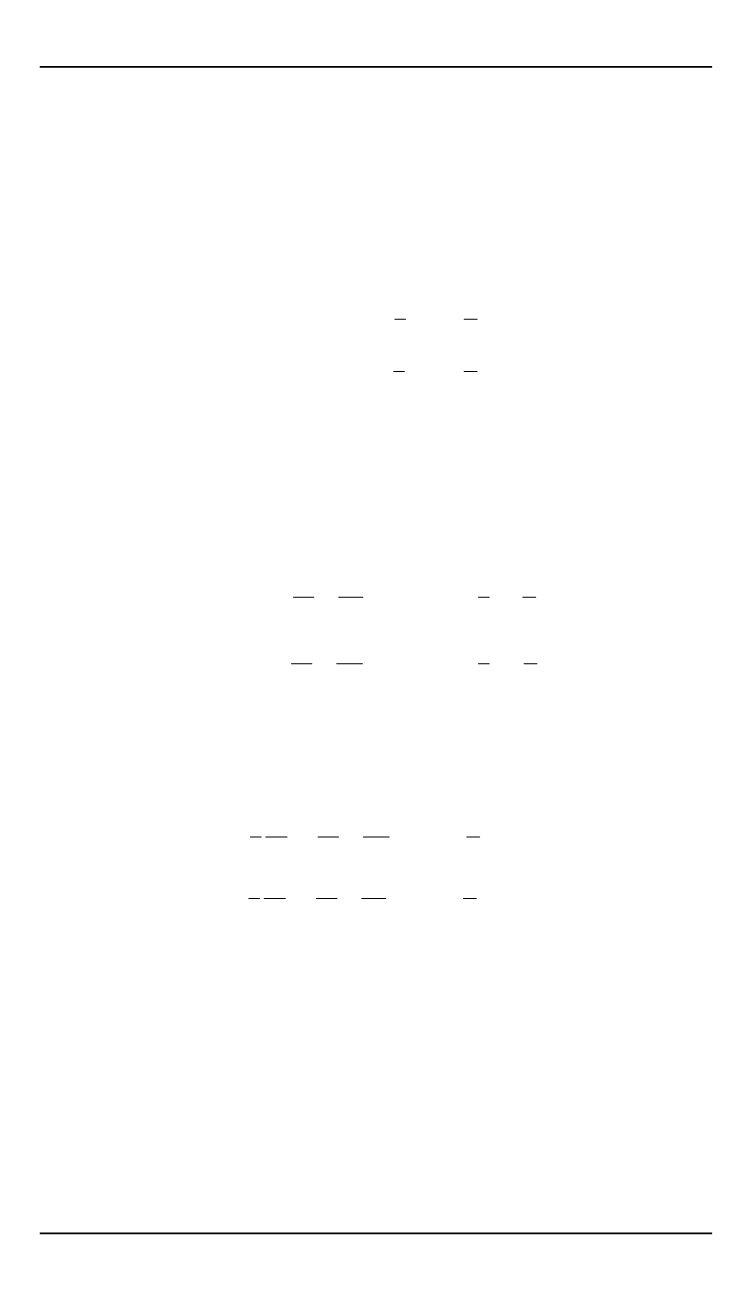
Цилиндрические оболочки конечной длины под внешним давлением
принимают вид
˙
e
j
= ˙
5
j
x
(˙
e
0
j
= 0)
,
˙
e
= ˙
e
0
+ ˙
5 x
,
где
˙
e
0
— скорость деформации срединной поверхности в направлении
оси ;
˙
5
j
и
˙
5
— скорости изменения главных кривизн.
Вычислим скорости изменения кривизн в продольном направле-
нии в точках (
= 0
,
j
=
p
/
2
),
(
= 0
,
j
= 0)
соответственно:
˙
5
= ˙
′′
( ) =
1
4
˙
b
( )
(︁
p
)︁
2
,
˙
5
= ˙
′′
( ) =
−
1
4
˙
a
( )
(︁
p
)︁
2
.
Из выражений (12) получим выражения для напряжений:
средние значения напряжений в точках и соответственно
˙
s
01
= 2
L
−
1
˙
e
01
,
˙
s
02
= 2
L
−
1
˙
e
02
,
главные напряжения в окружном направлении в точках и
s
j
=
L
−
1
[︂
2
(︂
1
)︂
x
+ ˙
e
01
+
1
4
˙
b
(︁
p
)︁
x
]︂
,
s
j
=
L
−
1
[︂
2
(︂
1
)︂
x
+ ˙
e
02
−
1
4
˙
a
(︁
p
)︁
x
]︂
.
Ограничимся подробным изучением этапа I деформирования сре-
динного сечения.
Вычислим моменты
j
(в окружном направлении) в точках и :
=
2
3
ℎ
3
L
[︂
2
(︂
1
)︂
−
(︁
p
)︁
2
˙
a
( )
]︂
,
=
2
3
ℎ
3
L
[︂
2
(︂
1
)︂
−
(︁
p
)︁
2
˙
b
( )
]︂
.
Коэффициент имеет следующие значения: при шарнирном закреп-
лении равен
1
/
4
, при жесткой заделке —
1
/
2
.
Из геометрических соотношений (см. рис. 1,
a
) на этапе I имеем
зависимости
( ˙
3
≈
0)
:
( ) =
−
(
−
) cos
3
⇒
˙ ( ) = ˙ (1
−
cos
3
) + ˙ cos
3
,
b
( ) =
0
−
( )
⇒
˙
b
=
−
˙ ( ) =
−
(︀
˙ (1
−
cos
3
) + ˙ cos
3
)︀
,
( ) = (1
−
sin
3
) + sin
3
⇒
˙ ( ) = ˙ (1
−
sin
3
) + ˙ sin
3
,
a
( ) = ( )
−
0
⇒
˙
a
( ) = ˙ (1
−
sin
3
) + ˙ sin
3
.
9