В.И. Ванько
по касательной к соответствующим образующим
′
и
′
(
′′
и
′′
) при любом закреплении концов оболочки (рис. 5).
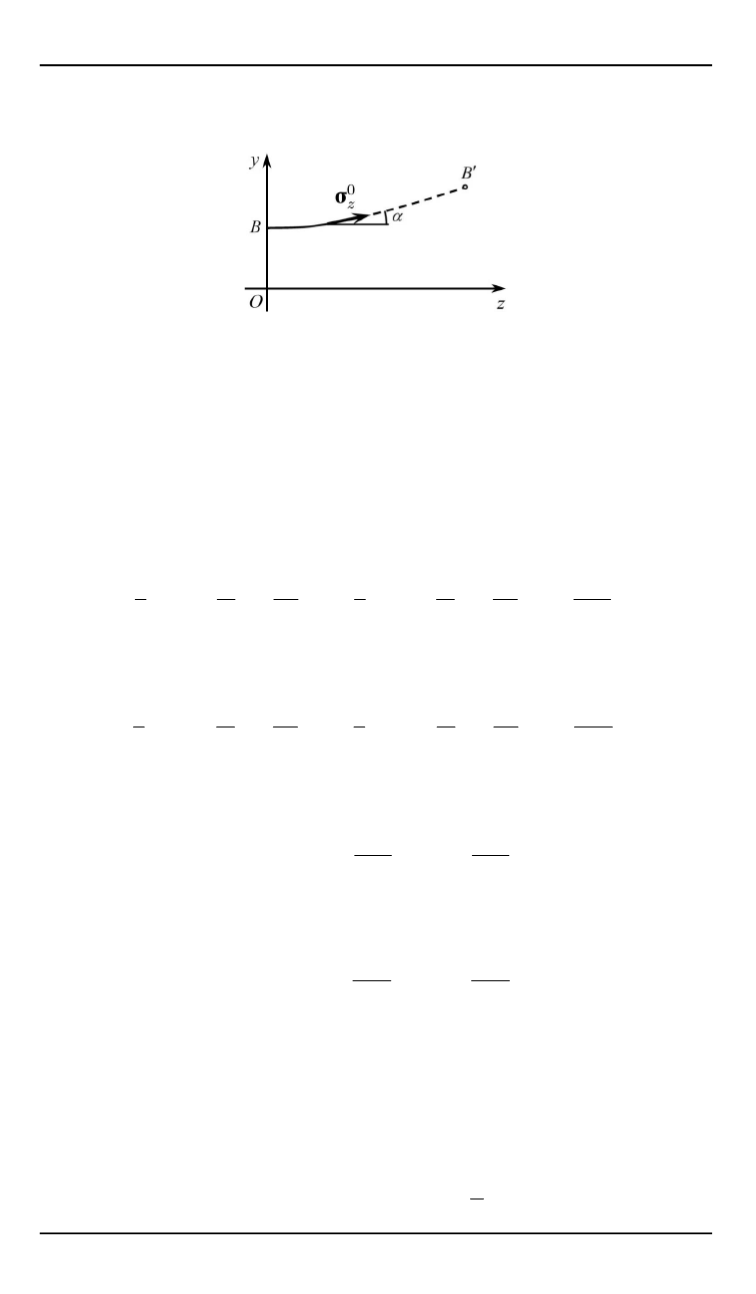
Рис. 5.
Образующая оболочки и вектор внутреннего напряжения
Спроецируем вектор
s
0
на ось (
):
s
0
=
⃒ ⃒
s
0
⃒ ⃒
sin
a
≈
⃒ ⃒
s
0
⃒ ⃒
tg
a
=
s
0
′
( )
,
s
0
≈
s
0
′
( )
.
Найдем средние по длине оболочки значения производных
′
( )
,
′
( )
. При шарнирном закреплении и жесткой заделке получаем для
′
1
∫︁
0
b
( )
p
2
sin
p
2
=
1
∫︁
0
b
( )
p
2
sin
p
=
b
( )
,
для
′
1
∫︁
0
a
( )
p
2
sin
p
2
=
1
∫︁
0
a
( )
p
2
sin
p
=
a
( )
.
Итак, силы в точке (рассматриваем всю образующую
′′
′
)
2
( ) =
ℎ
∫︁
−
ℎ
2
s
0
b
( )
h
= 4
ℎ
b
( )
s
0
.
Аналогично в точке
1
( ) =
ℎ
∫︁
−
ℎ
2
s
0
a
( )
h
= 4
ℎ
a
( )
s
0
.
В точках и модули сил, возникающих от растяжения образу-
ющих, максимальны.
Примем, что силы
2
(
y
)
и
1
(
y
)
, распределенные по дугам и
соответственно, линейны по углу
y
(рис. 4):
2
(
y
) =
2
(
3
−
y
)
,
0
6
y
6
3
,
1
(
y
) =
1
y
,
0
6
y
6
p
2
−
3
.
(5)
6


