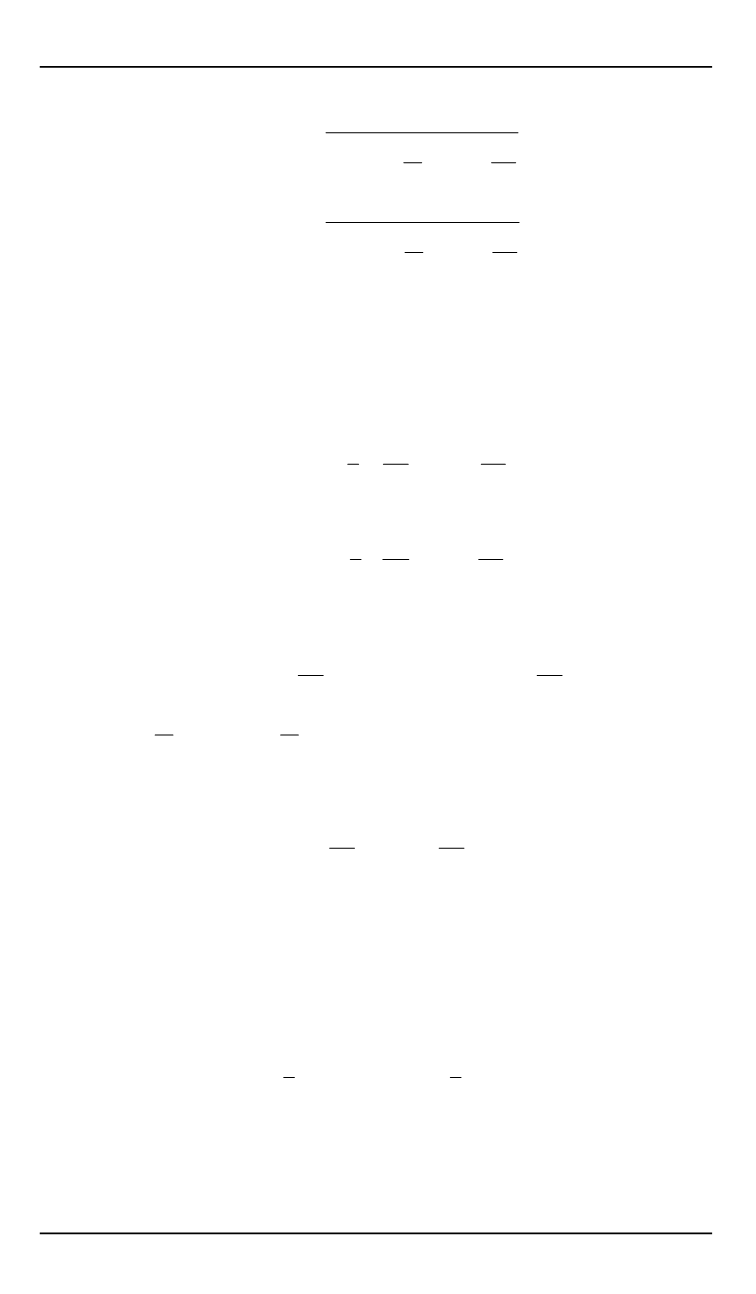
Цилиндрические оболочки конечной длины под внешним давлением
Текущие длины этих образующих (см. рис. 2)
2
( ) =
∫︁
0
√︂
1 +
b
2
(︁
p
2
)︁
2
sin
2
p
2
,
1
( ) =
∫︁
0
√︂
1 +
a
2
(︁
p
2
)︁
2
sin
2
p
2
.
(4)
Если принять, что рассматриваются такие перемещения и пара-
метры оболочки, для которых выполняются неравенства
/
2
<
1
/
5
,
0
/
2
<
1
/
5
, можно воспользоваться формулой бинома с точностью
примерно
5 %
, и выражения (4) существенно упрощаются:
2
( ) =
∫︁
0
(︃
1 +
1
2
(︂
bp
2
)︂
2
sin
2
p
2
)︃
,
1
( ) =
∫︁
0
(︂
1 +
1
2
(︁
ap
2
)︁
2
sin
2
p
2
)︂
.
После вычисления интегралов имеем
2
( ) =
(︂
1 +
2
1
4
)︂
,
1
( ) =
(︂
1 +
2
2
4
)︂
.
Здесь
1
=
p
2
b
( )
,
2
=
p
2
a
( )
.
Соответствующие деформации в точках срединной поверхности на
образующих
′
и
′
при шарнирном закреплении
e
0
=
2
1
4
,
e
0
=
2
2
4
.
Так как в плоскости
сечение оболочки может изгибаться, де-
формациями растяжения-сжатия срединной поверхности пренебрега-
ем:
e
0
y
= 0
.
Скорости деформации в точках сечений плоскостями ,
и
имеют значения (производные вычисляются по времени либо по
параметру нагружения)
˙
e
0
=
1
2
1
˙
1
,
˙
e
0
=
1
2
2
˙
2
.
Деформации и их скорости обусловят возникновение растягивающих
напряжений
s
0
в точках образующих
′
и
′
срединной поверхно-
сти. Считаем, что напряжения
s
0
равномерно распределены по длине
образующих оболочки, причем вектор
s
0
в любой точке направлен
5