И.Ю. Владимиров, Н.Н. Корчагин, А.С. Савин
10
же проходящая через точку (1 1),
является касательной к
2
.
Уравне-
ние
0 1 2
(
) 0
f E E
задает в первом квадранте отрезок
1
,
соединяющий
точки (1 0)
и (0 1).
Кривая
2
и отрезок
1
разбивают первую четверть
на три области. В области
2
,
расположенной над
2
,
выполняются
неравенства
2 1 2
(
) 0
f E E
и
0 1 2
(
) 0;
f E E
в области
1
,
находящейся
между
2
и
1
,
функция
2 1 2
(
) 0,
f E E
а
0 1 2
(
) 0;
f E E
наконец, в
области
0
,
являющейся треугольником с вершинами в точках
(0 0),
(1 0),
(0 1),
функции
2 1 2
(
) 0,
f E E
0 1 2
(
) 0.
f E E
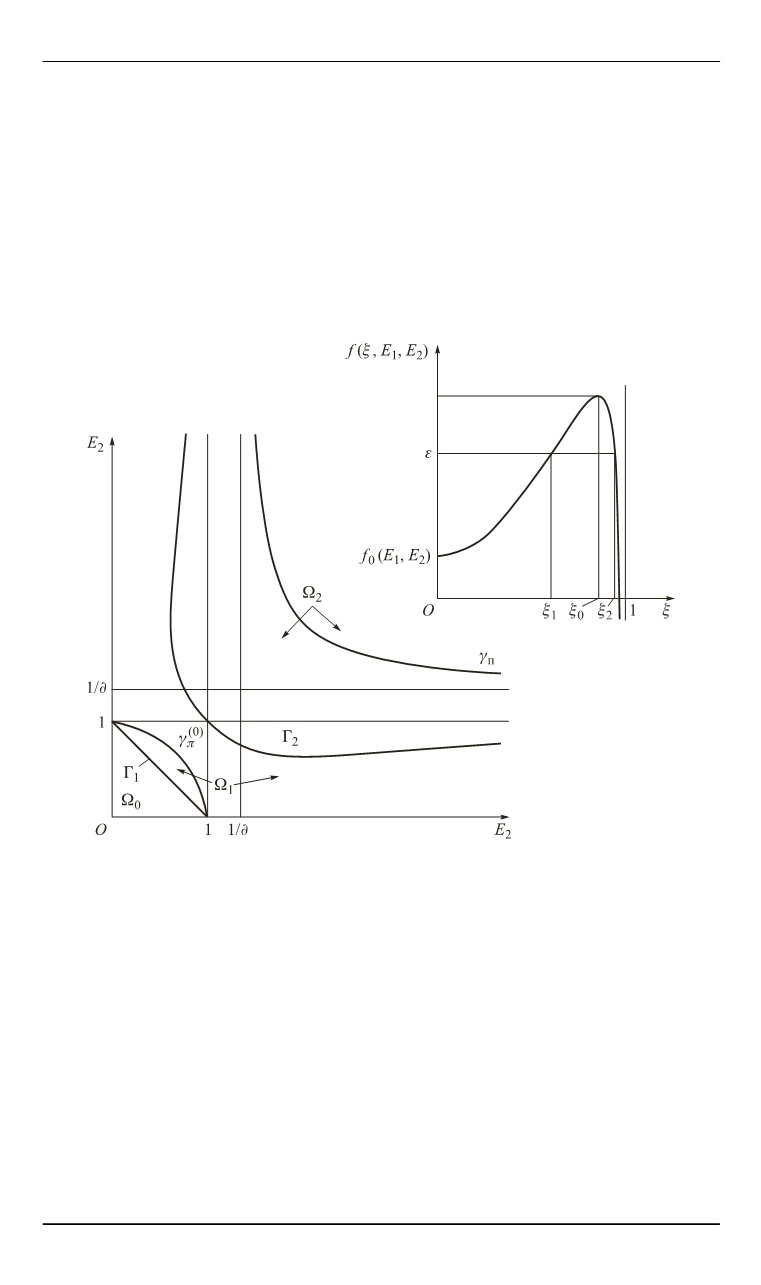
Рис. 2. Графическое представление анализа поведения и свойств функ-
ции
1 2
(
)
f
E E
Теперь о количестве корней уравнения (18) на интервале (0;1) в
условиях
E
1
> 0,
E
2
> 0 и
0 1.
Сначала сформулируем критерии
существования двух корней. Ясно (см. рис. 2), что этот случай реали-
зуется только тогда, когда функция
1 2
(
)
f
E E
имеет локальный
максимум в точке
0
(0 1)
и значение параметра
лежит внутри
интервала
0 1 2
0 1 2
(
) (
)
f E E f
E E
, т. е.
2 1 2
0 1 2
1 2
(0 1)
(
) 0;
(
)
max (
)
f E E
f E E
f
E E


