С.Д. Попов
6
лучаемой из исходной с помощью
N
последовательных элементар-
ных вращений):
(
)
.
1
...
,
n m n
n m
A
= ϕ ϕ
r
r
где
,
1,
j
j
N
ϕ =
— эйлеровы углы.
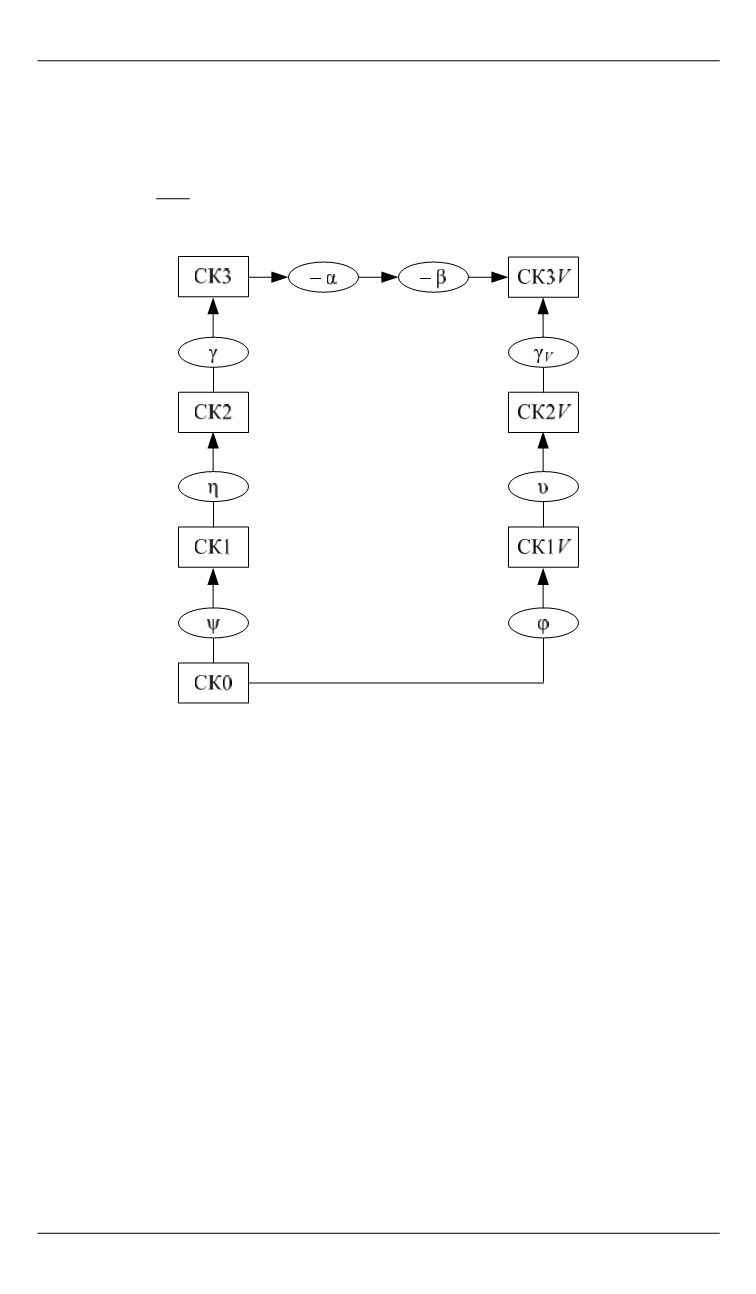
Рис. 5.
Схема преобразования систем координат
При последовательном переходе от системы координат СК1 к си-
стеме координат СК
h
через промежуточные системы СК2, ..., СК(
h
–
1) результирующая матрица перехода задается формулой
1;
( 1);
2;3 1;2
...
.
h
h h
A A
A A
−
=
⋅ ⋅
⋅
Матрица обратного перехода определяется формулой
[ ]
т
;1 1;
,
h
h
A A
=
иначе говоря, обратное вращение задается теми же матрицами с за-
меной одноименных углов на их отрицательные значения. Другой
способ получения матрицы обратного элементарного вращения со-
стоит, как известно, в транспонировании матрицы прямого элемен-
тарного поворота.
Строка матрицы
(
)
0;3
А
γ η ψ
, задающей переход от нормаль-
ной системы координат к связанной (СК0→СК3), — строка из ком-
понентов одного из единичных векторов (ортов) системы координат
СК3 в системе координат СК0. Столбец этой же матрицы является


