А.В. Копаев, С.К. Соболев
8
Точные значения корней (с пятью знаками после запятой):
1
2
3
2,11491,
0, 25410,
1,86081,
x
x
x
т. е. ошибка порядка одной сотой.
Далее подробно исследуем
комплексные
корни уравнения (5)
при
0 3
3 .
4
p p
Сначала получим связь между действительной и
мнимой частями этих корней с учетом того, что
.
p
Имеем
2
2
2
2
2
2
2
2
2
2
1 (
)
2
x iy
x
y
p z
x iy
x y
i xy
z
x y
x y
x y
,
откуда, поскольку
Im( ) 0,
p
получим
2
2
1
2
0
y x
x y
. В ком-
плексной плоскости это объединение прямой
0
y
(соответствую-
щей вещественным корням) и кривой
2
2
2
1
1
2
2
x
y
x
x y
x
.
(10)
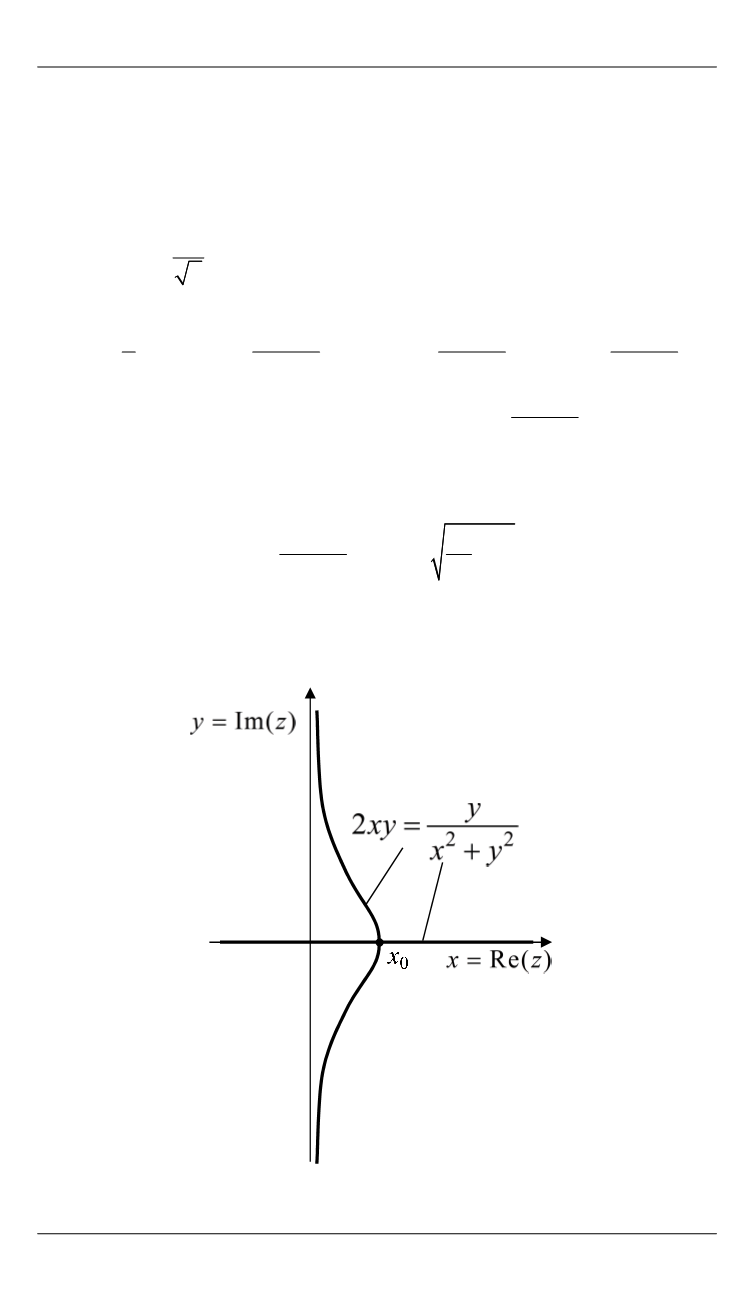
Эта линия (рис. 4) — траектория графика двузначной функции
( )
z z p x iy
комплексных корней уравнения (5). Из (10) следует,
Рис. 4.
Линия комплексных корней кубического уравнения
на комплексной плоскости
0


