Графическое и аналитическое исследование комплексных корней
3
Если же
( )
z f p
— комплексная функция комплексного аргу-
мента
,
i
p a ib re
то для ее графика понадобится вещественное
четырехмерное пространство, и поэтому изобразить ее график за-
труднительно. В этом случае для ее представления можно использо-
вать изображения на комплексной плоскости
z
образов линий
Re( ) const, Im( ) const,
const
p
p
p
и
arg( ) const.
p
Объектом нашего изучения будет кубическое уравнение с дей-
ствительными (или комплексными) коэффициентами. Как известно,
даже если все коэффициенты вещественны, то некоторые корни мо-
гут быть комплексными. Кубические уравнения часто возникают при
решении прикладных задач, например при решении линейных одно-
родных дифференциальных уравнений с постоянными коэффициен-
тами [1]. Используемый аппарат — элементарные сведения о ком-
плексных числах, доступные даже школьнику [2–4], а также теория
предела и дифференциальное исчисление функций одной действи-
тельной переменной.
Рассмотрим кубическое уравнение
3
2
0
a b c d
(1)
с комплексной неизвестной
и с действительными или комплексны-
ми коэффициентами
, , , ,
a b c d
причем
0.
a
Из основной теоремы
алгебры [5] следует, что это уравнение имеет три (не обязательно
различных) корня
1 2 3
, ,
z z z
(вообще говоря, комплексных), таких, что
справедливо разложение:
t
0
y
x
t
Г
L
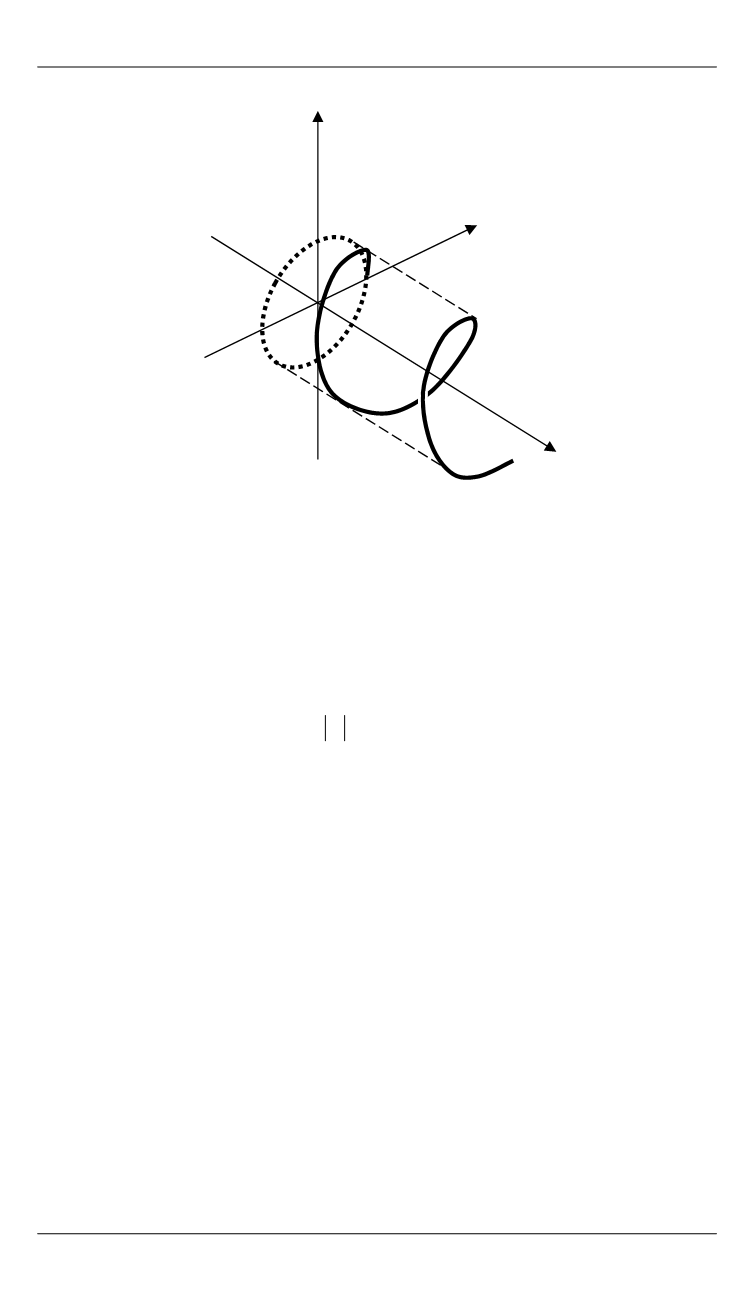
Рис. 2.
График равномерного вращения точки вокруг точки
О
и его траектория


