А.В. Копаев, С.К. Соболев
6
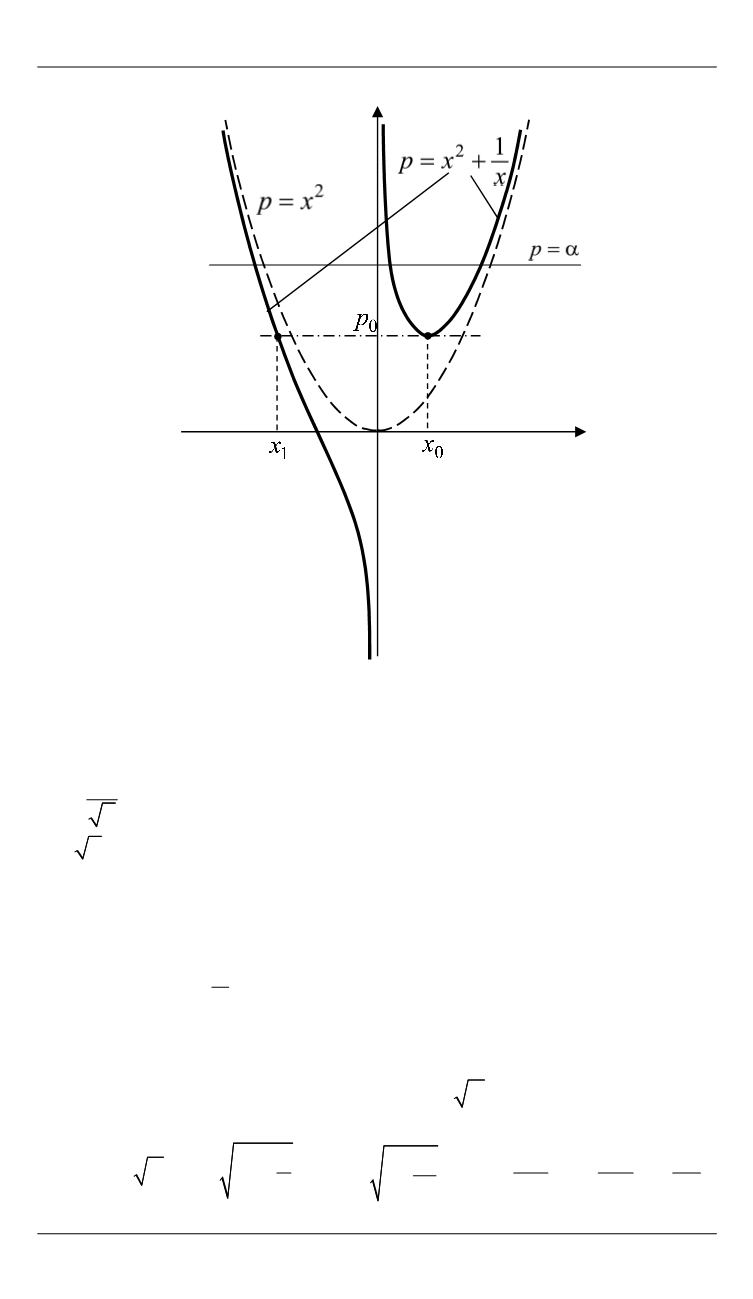
Рис. 3.
График зависимости параметра
p
и вещественных корней кубиче-
ского уравнения
При
0
p p
уравнение имеет двукратный вещественный корень
0 3
1
2
x
и простой вещественный отрицательный корень
0
2
x x
3
4.
Если же
0
,
p p
то уравнение (5) имеет только один веще-
ственный (отрицательный) корень и, следовательно, еще два ком-
плексных взаимно сопряженных корня
2,3
z x iy
. Для этого един-
ственного вещественного отрицательного корня
( )
x p
справедлива
асимптотика:
1~
x
p
при
.
p
Найдем более подробные асимптотические разложения веще-
ственных корней уравнения (5) при
.
p
Пусть
.
p
Для корня
3
( ) ~
x x p p
найдем главную часть
разности:
2
3
3
2
3
1
1
1
1
1 ~
~
1 1
2
2
2
x x p x x
x
x
x
x
x
p
x
.
х
р
0 –1


