Графическое и аналитическое исследование комплексных корней
11
Поэтому они, как функции
( )
r p
и
( ),
p
задаются параметрически:
3
2
1 ,
1
2
0;
1
2
4
2
r
t
t
p t
t
3
2
1
arctg
1,
2
.
1 4
2
t
p t
t
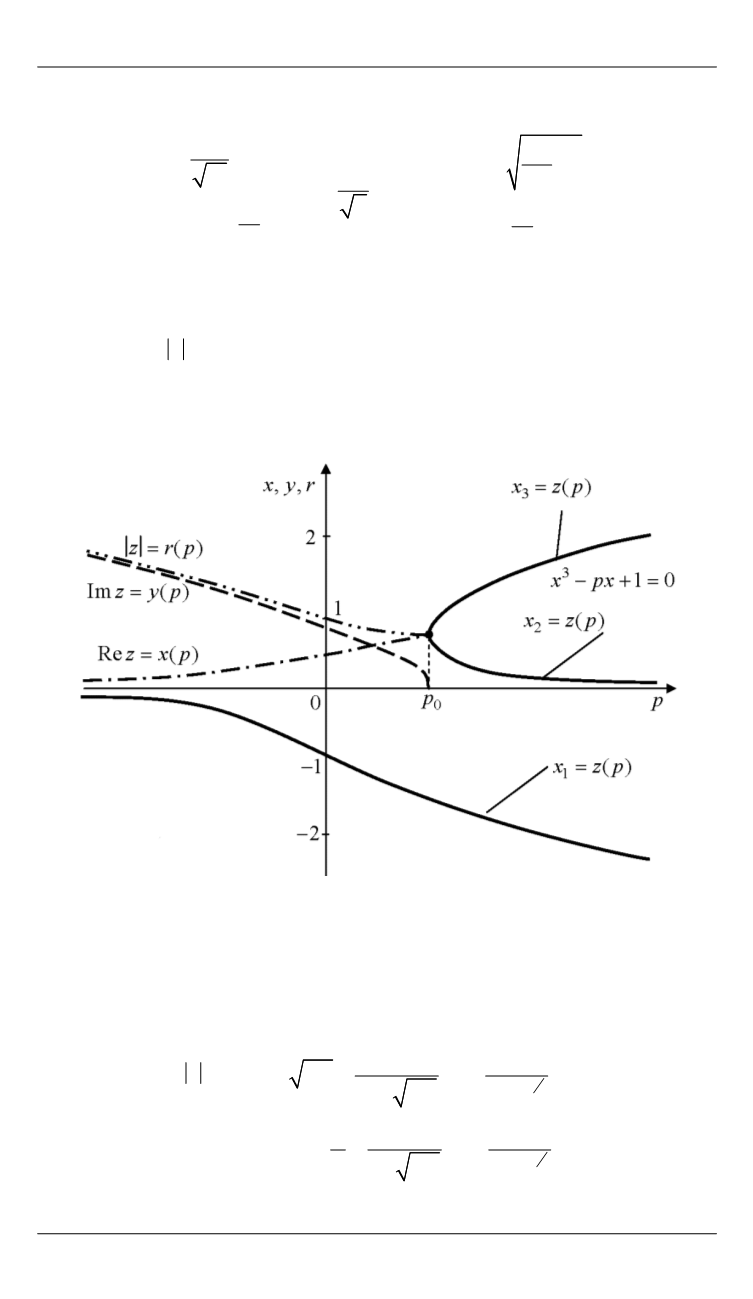
Для комплексного корня
i
z x iy r e
с положительной мни-
мой частью на рис. 6 приведены графики функций
Re( ) ( ),
z x p
Im( ) ( ),
( )
z y z z r p
и
arg( ) ( )
z
z
, там же представлены графики
вещественных корней
1 2 3
, ,
x x x
кубического уравнения (5) в зависи-
мости от параметра
р
.
Рис. 6.
Графики зависимости от параметра
р
вещественных корней,
действительной и мнимой частей, а также модуля комплексных корней
кубического уравнения
Для модуля и аргумента комплексного корня тоже можно полу-
чить асимптотические представления при
:
p
5
2
3
2
2
1
1
( )
,
2
1
1
arg( ) ( )
.
2 4
z r p
p
o
p p
p
z
p
o
p p
p
(12)


