А.В. Копаев, С.К. Соболев
2
Пусть
( )
( ) ( ),
z f t
z x iy g t ih t
t T
R
— комплексная
(комплекснозначная) функция вещественного аргумента
t
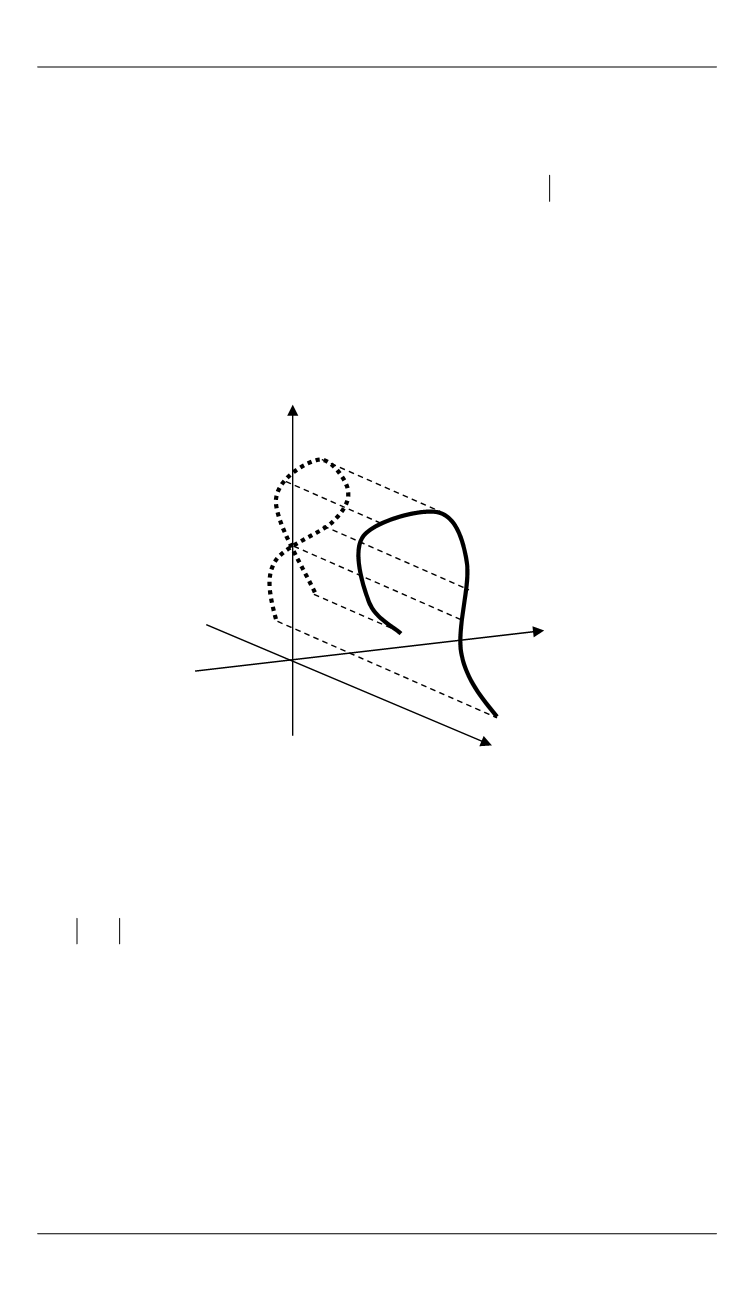
. График этой
функции «лежит» в трехмерном пространстве. Под графиком этой
функции понимается множество точек
( ) ( ; )
,
( )
f
t w t T w f t
.
Иначе говоря, график рассматриваемой функции — мно-
жество точек
3
( ) {( ; ; )
|
,
f
t x y
t T
( ),
( )},
x g t y h t
которое
можно изобразить на плоскости в виде его проекции (рис. 1). Проекция
этого графика на комплексную плоскость есть
траектория
функции
( ),
z f t
т. е. линия
L
на плоскости
( , ),
x y
заданная параметрически:
( ),
x x t
( ).
y y t
Кроме того, можно отдельно изобразить на плоскости графики
«координатных» функций:
Re ( ( )) ( ),
x
f t
g t
Im( ( )) ( ),
y
f t
h t
( )
r f t
и
arg( ( )),
f t
которые также дают представление о поведе-
нии функции
( ).
z f t
Например, равномерное вращение точки на
комплексной плоскости вдоль окружности радиусом
R
с центром в
точке ноль из начального положения
0
0
z R i
с угловой скоростью
описывается функцией
cos ( ) sin ( ) .
i t
z Re R
t i
t
Графиком
этой функции является винтовая линия, а проекцией графика на ком-
плексную плоскость является траектория этой точки — окружность
радиусом
R
с центром в точке ноль (рис. 2). Координатные функции
здесь такие:
( )
cos( ), ( )
sin( ), ( )
const
x t
R t y t
R t r t
R
и
( )
.
t
t
x
y
0
t
Г
L
Рис. 1.
График комплекснозначной функции и его проекции на комплекс-
ную плоскость


