Постановка специального курса «Марковские модели систем с взаимодействием»
9
удовлетворяет второму уравнению Колмогорова [11]
2
2
2
2
1 2
0
2
( ; )
( ; )
( ; )
= (
)
(
)
i
i
i
F t s
F t s
F t s
s s
p s p s
t
s
s
с начальным условием
(0; ) = .
i
i
F s s
Для рассматриваемой автокаталитической реакции с кинетиче-
ской схемой
2
;
T T
0, 2
T
T
уравнение детерминированной мо-
дели имеет вид
2
1 2
0
2
0
( ) = (
) ( )
( ),
(0) =
x t
p p x t
x t
x x
(
( )
x t
— количество реагента
).
T
Решение имеет вид
0
2
(
)
p p
1 2
0 0
(
)
1 2 0
1 2
0
2 0
2 0
(
)
( ) =
.
( (
)
)
p p t
p p x
x t
p p
x e
x
(3)
Пусть
2
0
> .
p p
Из (3) следует, что детерминированная модель
( )
x t
выходит при
t
на стационарный уровень
c
=
x
1 2
0
2
(
) /
> 0.
p p
Случайный процесс
( )
t
длительное время
находится в окрестности точки
c
,
x
но с вероятностью
1
попадает
независимо от значений параметров в поглощающее состояние 0.
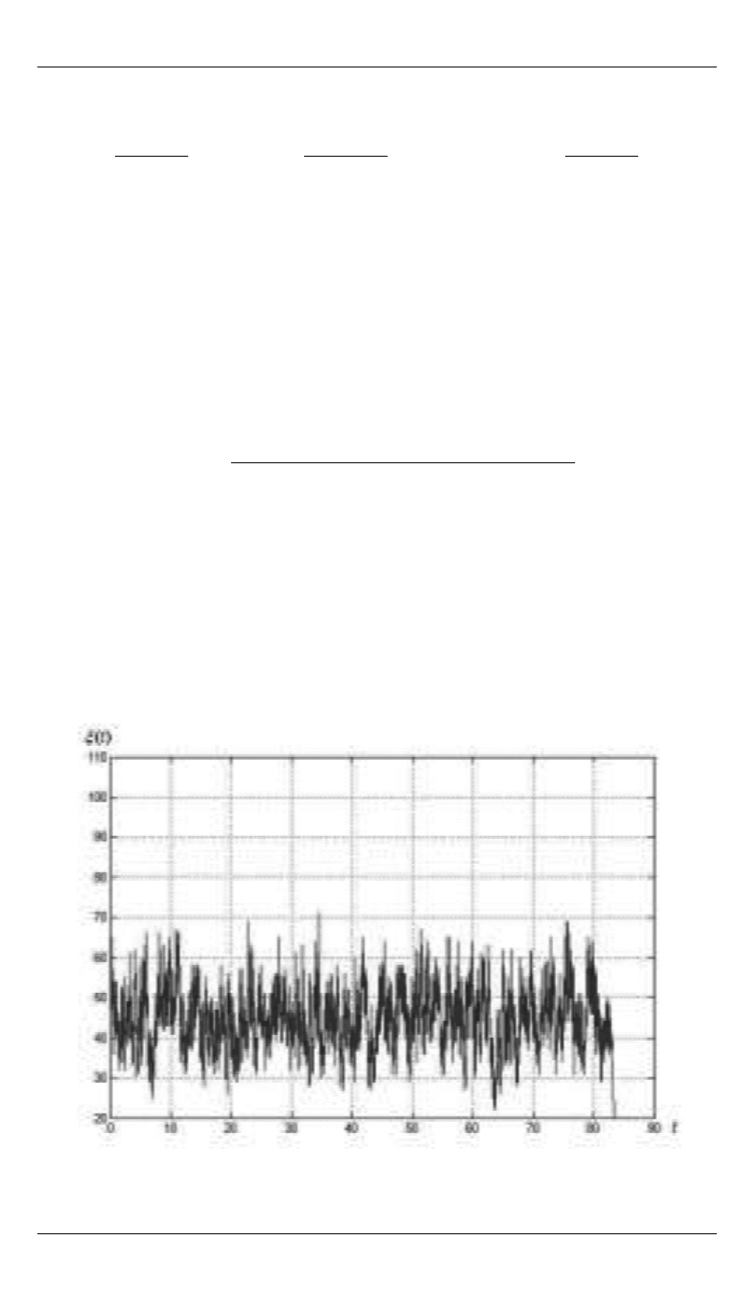
Пример такой реализации процесса приведен на рис. 2.
Рис. 2.
Случайный процесс
( )
t
с вероятностью 1 остановится в состоянии 0


