Постановка специального курса «Марковские модели систем с взаимодействием»
11
переходные вероятности
1 2
1 2
( ,
)
1
2
1 2
1
2
1 2
( ,
)
( ) = P{( ( ),
( )) = ( ,
) | ( (0),
(0)) = ( ,
)}
P t
t
t
которого при
0
t
представимы в виде
2
1
0
( > 0,
> 0,
> 0)
1 2
1
2
1 2
1
2
1 2
1 2
1 2
1 2
( ,
)
2 1 2
(
1,
1)
( ,
)
1 1
( 1,
)
( ,
)
0
( ,
1)
( ,
)
2 1 1
2 1
0
( ,
)
( ) =
( ),
( ) =
( ),
( ) =
( ),
( ) = 1 (
)
( ).
P
t
t o t
P t
t o t
P t
t o t
P t
t o t
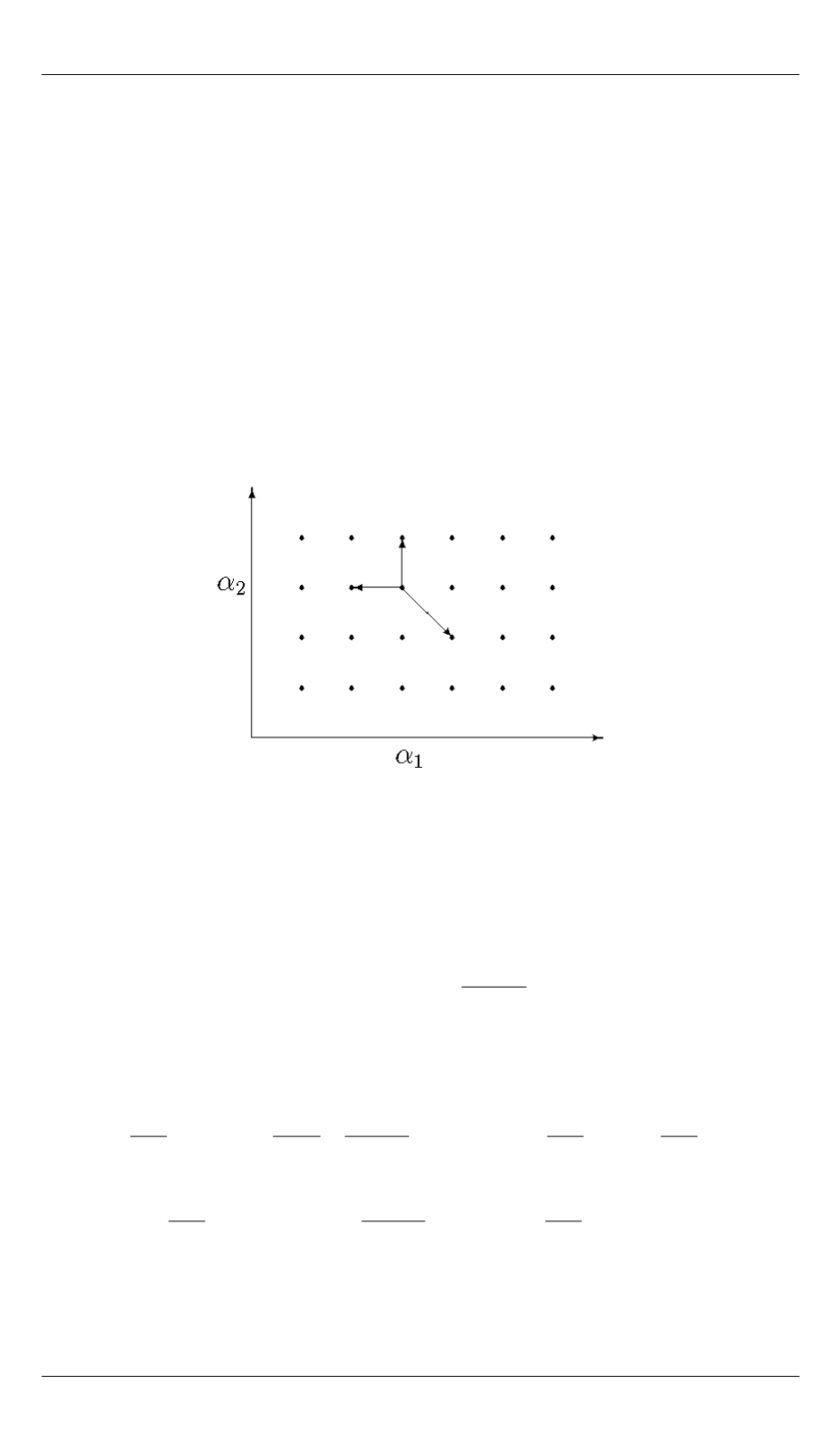
Скачки марковского процесса
1
2
( ( ), ( ))
t
t
изображены на рис. 4.
Рис. 4.
Скачки двумерного марковского процесса
1
2
( ( ),
( ))
t
t
на фазовой
плоскости
Экспоненциальная (двойная) производящая функция переходных
вероятностей
1
2
| | 1, | | 1
s
s
1 2
1 2
1 2
1 2
1 2 1 2
( ,
)
1 2
1 2 1 2
1 2
( , )
,
, ,
=0 1 2
( ; , ; , ) =
( )
! !
z z
F t z z s s
P t s s
удовлетворяет первому и второму уравнениям Колмогорова [11]
2
2
2 1 2
1 1
0
2
1
1 2
1
2
2
2
2 1
1 2
1
1
0 2
1 2
1
=
,
= (
)
(1 )
(
1)
z z
z
t
z
z z
z
z
s s s
s
s
t
s s
s
с начальным условием
1 1 2 2
1 2 1 2
(0; , ; , ) =
.
z s z s
z z s s e


