А.В. Калинкин
12
Случайный процесс интерпретируется как модель распространения
инфекции в популяции с двумя типами особей: тип
1
T
— инфициро-
ванные; тип
2
T
— восприимчивые. Процесс
1
2
( ( ), ( ))
t
t
введен в [25]
как модель повторяющейся эпидемии и обобщает марковский процесс
эпидемии Бартлетта — Мак-Кендрика допущением, что количество
восприимчивых особей пополняется извне иммиграцией. Для кинети-
ческой схемы
1
2
1
2
T T T
,
1
0
T
,
2
0
T
уравнения детермини-
рованной модели имеют вид (
1
( )
x t
— количество
1
T
,
2
( )
x t
— количе-
ство
2
)
T
1
2 1 2
1 1
2
2 1 2
0
=
;
=
x
x x
x
x
x x
(4)
с начальными условиями
0
1
1
(0) =
x
x
,
0
2
2
(0) =
x
x
.
Система нелинейных уравнений (4) исследована в [25] путем ли-
неаризации в окрестности точки стационарности
0 1 1 2
( / , / ).
При
некоторых условиях на параметры показано, что
1
( ),
x t
2
( )
x t
пред-
ставляют собой затухающие колебания — траектория на фазовой
плоскости
1 2
x Ox
есть спираль, накручивающаяся на точку стацио-
нарности.
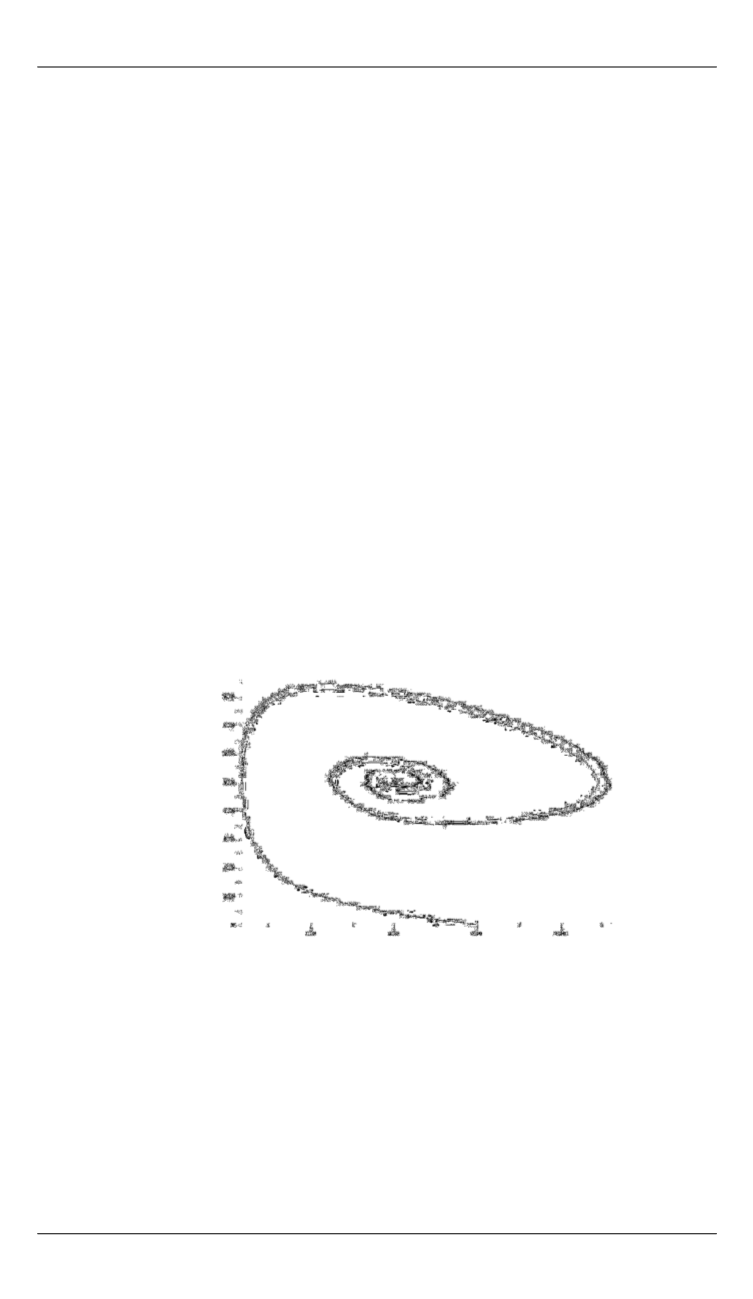
Рис. 5.
Пример детерминированной траектории и стохастической реализа-
ции для схемы
1 2
1
2 ,
T T T
1
0,
T
2
0
T
На рис. 5 приведен полученный методом Монте-Карло пример
спиралеобразной реализации марковского процесса; значения парамет-
ров
2
= 0,00005,
1
= 0,5,
0
= 1000
и начальные условия
1
= 3000,
2
= 0.
Процесс
1
2
( ( ), ( ))
t
t
длительное время находится в окрестно-
сти точки стационарности
0 1 1 2
( / , / ),
но с вероятностью
1
попада-


