А.В. Калинкин
10
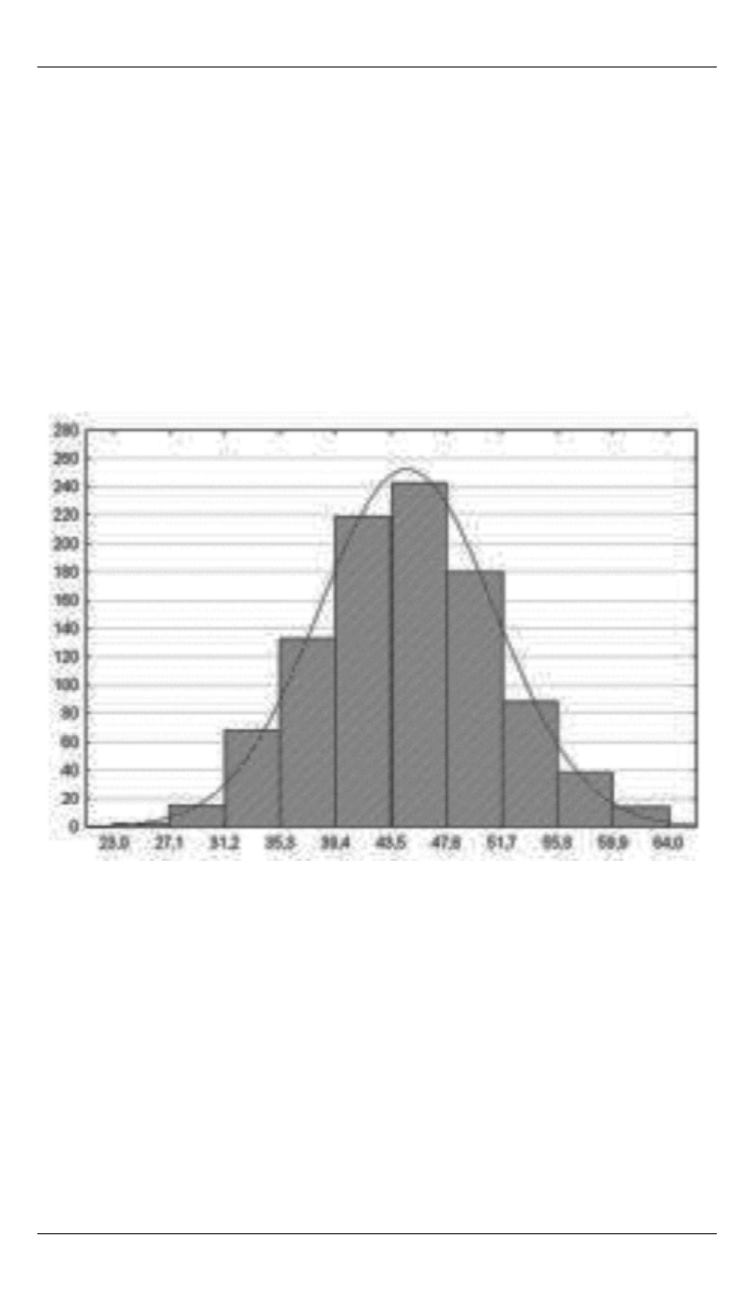
На рис. 3 приведена полученная методом статистических испы-
таний гистограмма условного распределения значения случайного
процесса (при условии непопадания случайного процесса в
0
), по-
строенная по
1000
реализаций процесса
( )
t
на фиксированном
промежутке времени
[0,50]
(рис. 1–3 даны при одинаковых значени-
ях параметров). Если точка стационарности
c
x
детерминированной
модели не близка к
0
, то гистограмма близка к плотности нормаль-
ного закона. В [7] доказано существование предельного условного
распределения
=
,
( ) = | ( ) > 0, (0) =
lim
t
j
q
t
j t
i
P
= 1, 2, ,
j
и
сделано предположение, что квазистационарное распределение близ-
ко к нормальному.
Рис. 3.
Гистограмма квазистационарного распределения
Пример. Спиралевидные реализации марковского процесса
рождения и гибели квадратичного типа
,
1
2
1
T T 2T
,
1
T 0
.
2
0 T
Приведем также пример двумерной стохастической модели
из типового расчета. Рассматривается однородный во времени мар-
ковский процесс рождения и гибели
1
2
( ( ), ( )),
[0, ),
t
t
t
на множестве состояний
2
1 2
1 2
={ = ( ,
),
,
= 0, 1, 2, },
N


