Исследование задачи аппроксимации траектории плоского разворота …
11
фик аппроксимации зависимости
0
( ( ))
x V t
аппроксимирующей функци-
ей
9
8
7
6
5
4
3
2
1
2
3
4
5
6
7
8
9
10
( )
.
f x p x p x p x p x p x p x p x p x p x p
= + + + + + + + + +
0
( ),M
V t
0
( ( )),м
x V t
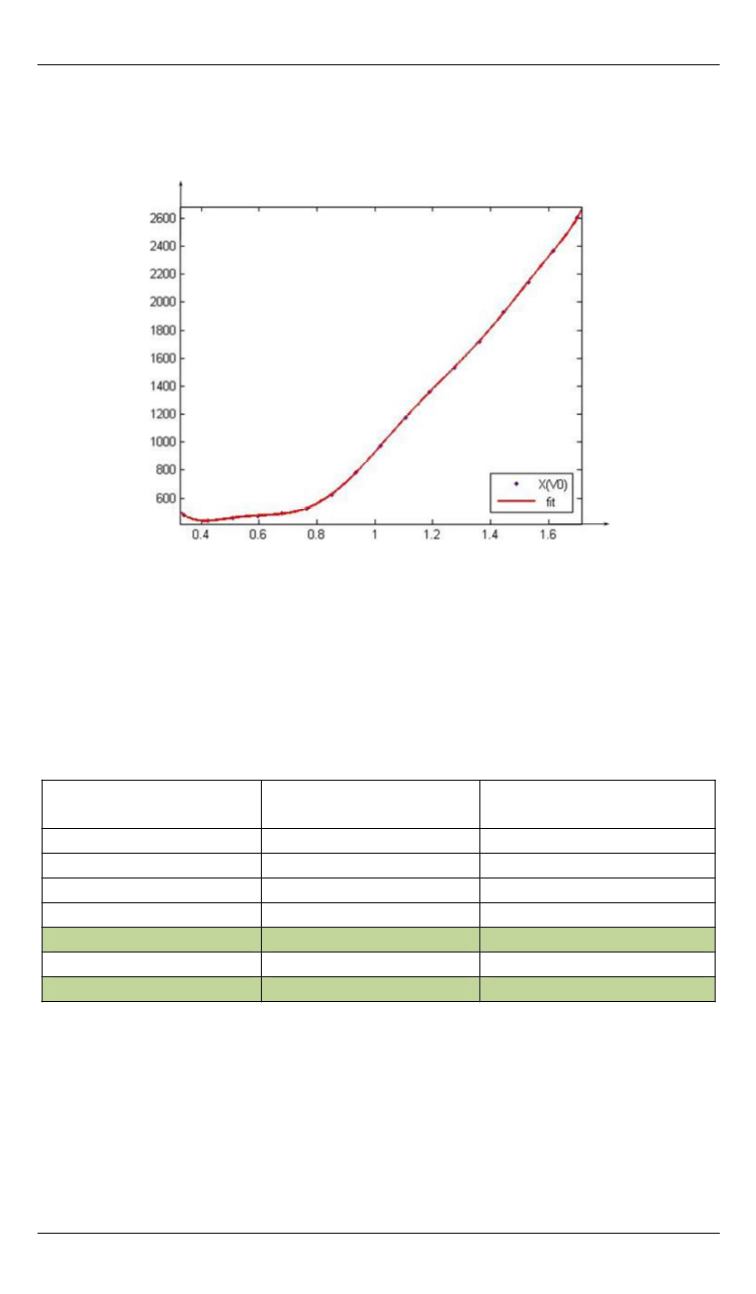
Рис. 12.
Аппроксимация зависимости
x
(
V
(
t
0
))
при
Ψ
(
t
k
) = 140° полиномом 9-й степени
В табл. 1 приводится сравнение точности аппроксимации при
выборе разных аппроксимирующих функций.
Таблица 1
Сравнение точностей аппроксимирующих функций
Аппроксимирующая
функция
SSE (сумма
квадратов ошибок)
RMSE (среднеквадра-
тическое отклонение)
Экспоненциальная
1,117e+005
92,7
Ряды Фурье
71,66
3,199
Гаусса
1,007e+005
84,81
Полином 5-й степени
4768
20,82
Полином 9-й степени
193,5
5,257
Синусоидальная
3163
39,77
Кубический сплайн
197
5,664
Аппроксимирующими функциями с наилучшей точностью явля-
ются полином 9-й степени и кубический сплайн.
5. Оценка погрешности параметров аппроксимированной
траектории и сравнение аппроксимирующих функций.
Погреш-
ность параметров траектории, построенной по аппроксимирующим
полиномам, рассматривается на основе результатов, полученных в
ходе моделирования исходной модели.


