А.А. Карпунин, Е.А. Зазирный
10
4) полином 5-й степени —
( )
5
4
3
2
1
2
3
4
5
6
f x p x p x p x p x p x p
= + + + + +
;
5) полином 9-й степени —
( )
9
8
7
6
5
4
3
2
1
2
3
4
5
6
7
8
9
10
f x p x p x p x p x p x p x p x p x p x p
= + + + + + + + + +
;
6) сумма синусоидальных составляющих;
7) кубические сплайны.
Общими критериями оценки являются сумма квадратов ошибок
SSE (Sum squared error) и среднеквадратическое отклонение RMSE
(Root-mean-square deviation), вычисляемые в процессе решения сред-
ствами MATLAB.
В аппроксимирующей функции рядами Фурье присутствуют гар-
монические составляющие, поэтому аппроксимированный вариант
может быть колебательным.
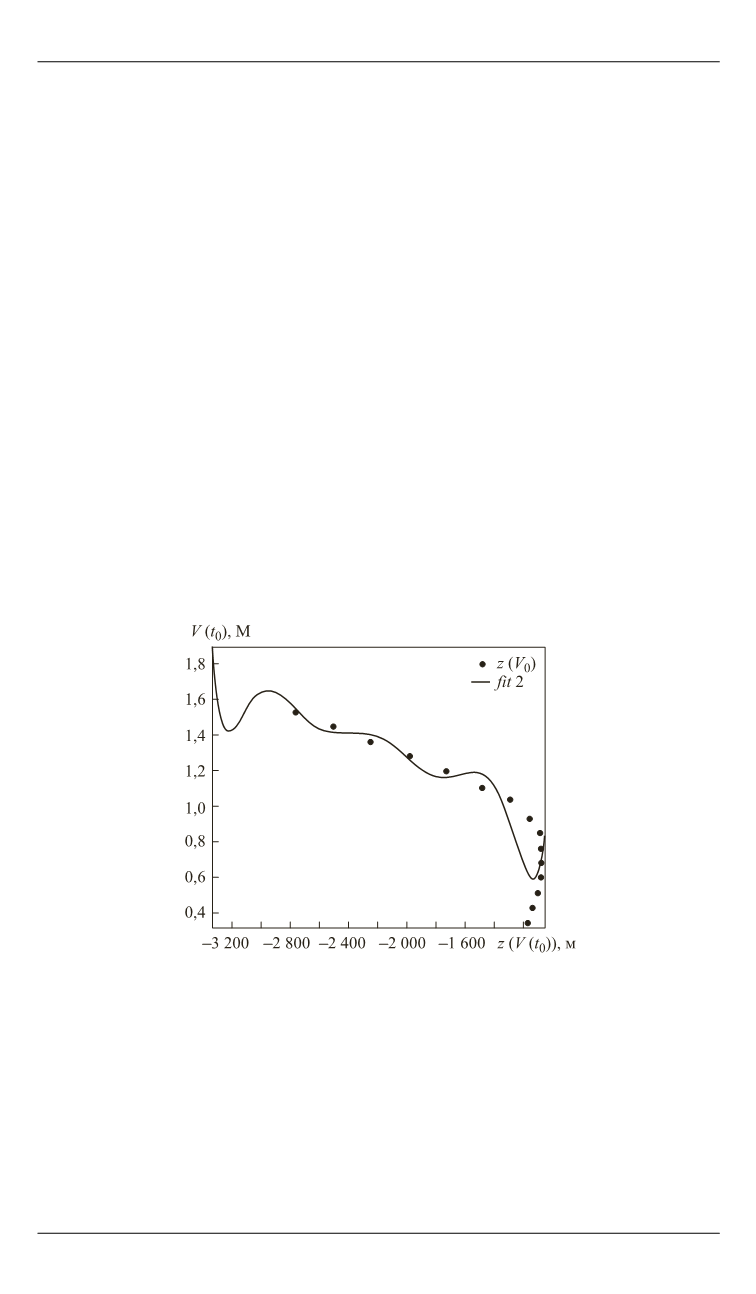
Например, на рис. 11 представлен график аппроксимации зави-
симости
0
( ( ))
z V t
аппроксимирующей функцией
( )
( )
( )
(
)
(
)
(
)
(
)
(
)
(
)
0 1
1
2
2
3
3
4
4
cos
sin
cos 2
sin 2
cos 3
sin 3
cos 4
sin 4 .
f x a a xw b xw a
xw b
xw
a
xw b
xw a
xw b
xw
= +
+
+
+
+
+
+
+
+
Рис. 11.
Аппроксимация зависимости
z
(
V
(
t
0
))
при
Ψ
(
t
k
) = 140° рядами Фурье
Характер функции колебательный, следовательно, аппроксима-
ция рядами Фурье в общем случае не может быть использована для
аппроксимации траектории.
Как пример также рассматривается аппроксимация поточечной
оценки траектории полиномом 9-й степени. На рис. 12 представлен гра-


