Исследование задачи аппроксимации траектории плоского разворота …
17
,м
Δ
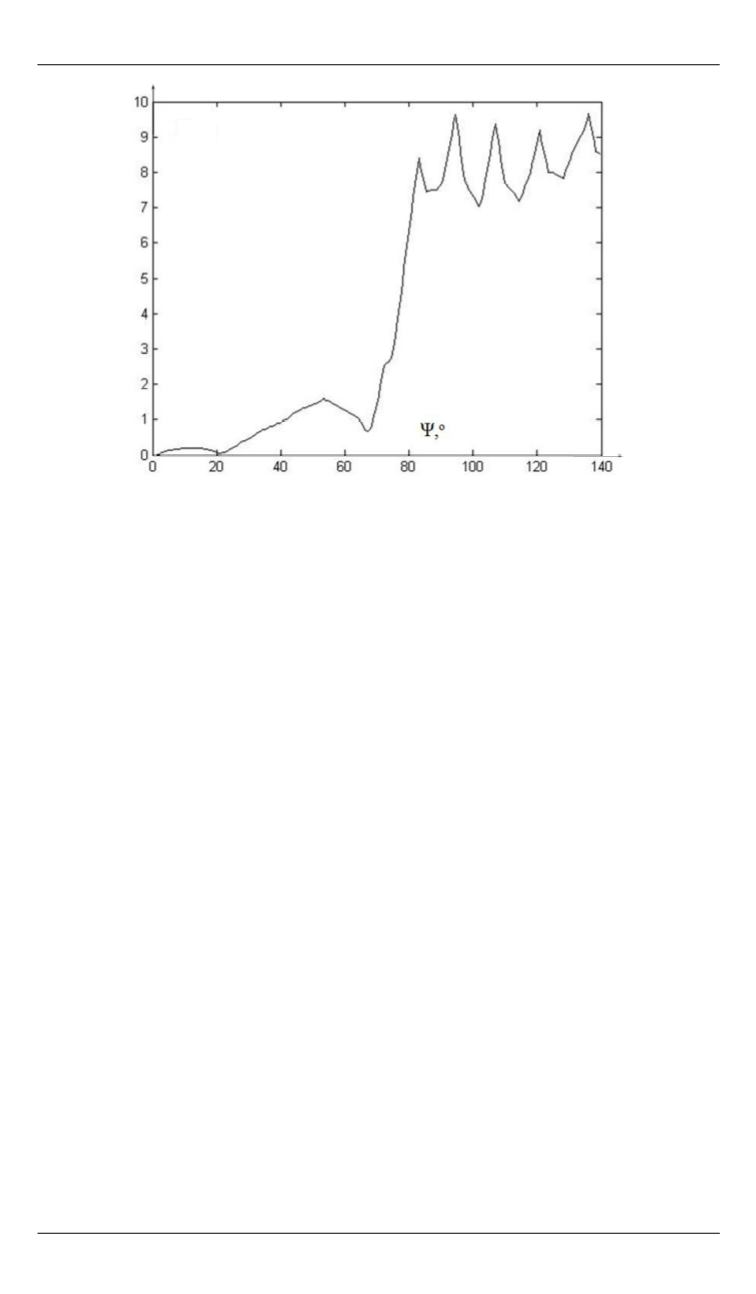
Рис. 17.
Зависимость
S
(
Ψ
) для линейной аппроксимации
Для работы алгоритма аппроксимации кубическими сплайнами в
рассматриваемом диапазоне исходных данных опорных траекторий
необходимо хранить 171 776 чисел типа double. На каждое число
данного типа необходимо 64 бита памяти. Следовательно, общий
объем требуемой памяти равен примерно 1,31 МБ (при использова-
нии значений в формате single — примерно 660 кБ).
Очевидно, что данные объемы памяти при использовании совре-
менной базы вычислительной техники являются весьма небольшими.
Использование же предложенного подхода позволит на порядки
уменьшить время расчета траектории разворота для любых исходных
данных в рассматриваемом диапазоне высот и скоростей.
Заключение.
В ходе выполнения данной работы получены алго-
ритмы построения траектории разворота летательного аппарата в
плоскости (расчет по исходной модели, расчет по аппроксимирую-
щей модели движения летательного аппарата в плоскости на основе
линейной и полиномиальной интерполяции).
Использование полиномиальной интерполяции кубическим
сплайном позволяет добиться наилучшего быстродействия для полу-
чения оценочной траектории разворота летательного аппарата в
плоскости при расчете модели в программной системе математиче-
ского пакета MATLAB при уровне погрешности, удовлетворяющем
постановке задачи.
По результатам выполнения данной работы может быть сделан
вывод, рекомендующий использование рассмотренного подхода для
оценки траектории движения в плоскости разворота с заданным
уровнем погрешности.


