Решение стационарных двумерных задач естественной конвекции…
7
2 2
2
2
2
2
2 2
2
2
2 2
2
2
1
1
(
)
(
)
2
2
1
1
1
1
(
)
(
)
(
)
(
)
0.
2
2
2
2
a x
b y
a
b
a x
b y
a x
b y
a
b
a
b
Большое количество примеров нормализованных областей слож-
ной формы приведено в [8].
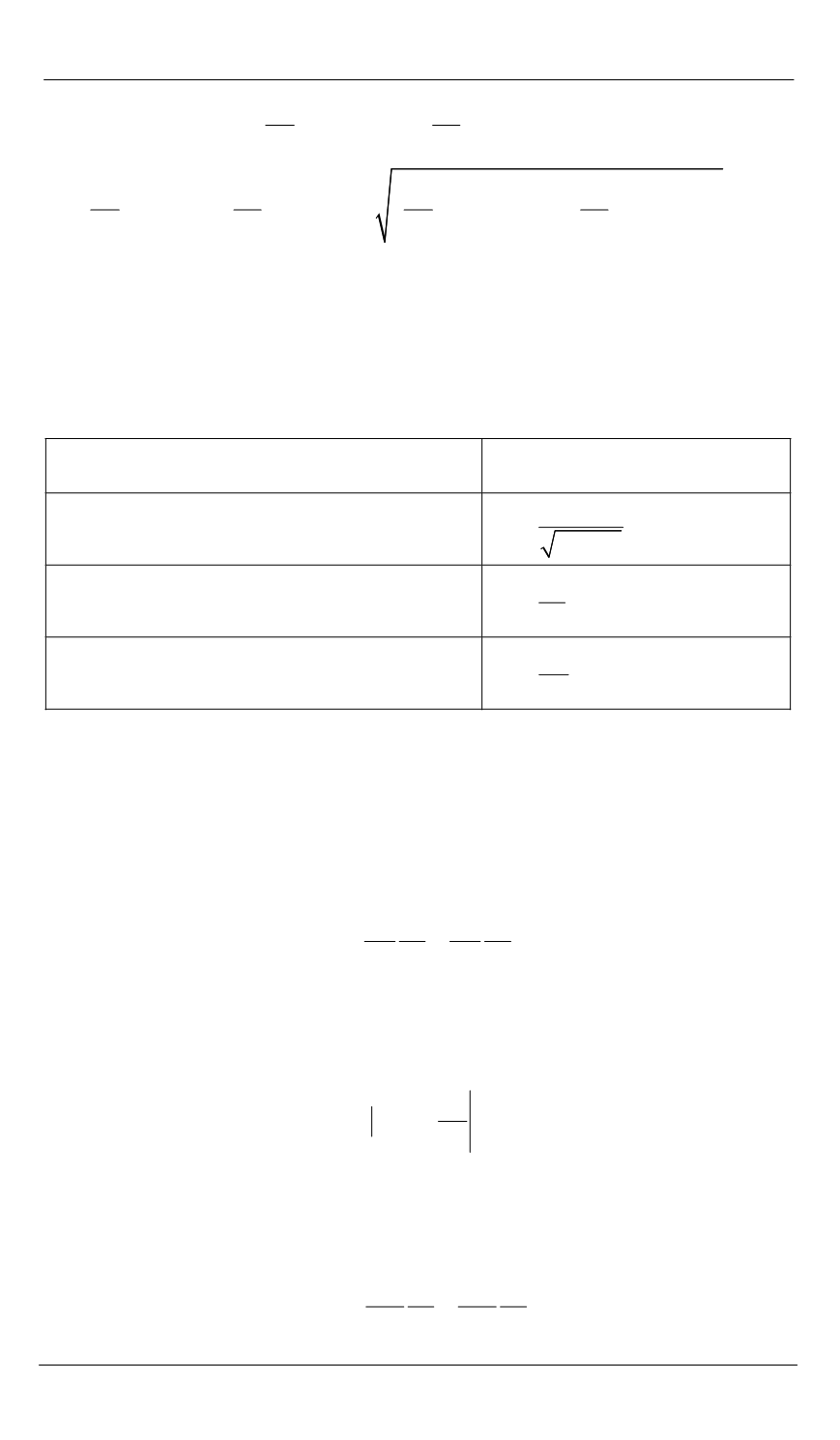
Таблица 1
Нормализованные уравнения границ простых
геометрических областей
Геометрический объект
Нормализованное уравнение
Прямая
0
ax by c
2 2
1 (
) 0
ax by c
a b
Полоса шириной 2
a
, параллельная оси
OY
2 2
1 (
) 0
2
a x
a
Окружность радиусом
R
с центром в точ-
ке (0, 0)
2 2
2
1 (
) 0
2
R x y
R
Нормализованное уравнение дает возможность строить пучки
функций, нормальная производная которых на границе области при-
нимает заданные значения. Для этого вводится линейный дифферен-
циальный оператор с переменными коэффициентами, зависящими от
формы области:
D
x x y y
.
(9)
Для произвольной достаточно гладкой функции
f
на границе об-
ласти
имеет место равенство
f
Df
n
.
Аналоги оператора
D
, соответствующие участкам
i
границы
, обозначим через
( )
i
i
i
D
x x y y
.


