М.А. Басараб
14
1
1
;
;
2
2
C
H
C
H C
f
X
X
.
Вместо (1) опять получим систему (17), а краевые условия (18)
примут вид
1 ,
,
:
0;
2
1 1
,
,
:
0.
2 2
H H
X Y
U V
L L
H Y
X
U V
L
n
n
n
(19)
Теперь представим безразмерную температуру в виде следующей
структуры решения (см. табл. 2):
1 2
1
2
1
2
1
0
1
2
(
)
(
)
,
N
n
n
n n
n
n
g
g
c
X X Y Y
. (20)
Здесь
2
2
2
1
2
2
1 ;
.
4
L H
X
Y
H L
Структуры решения для функции тока и вихря запишем в виде
(15), (16) соответственно, с учетом того, что
1
2
.
а
б
в
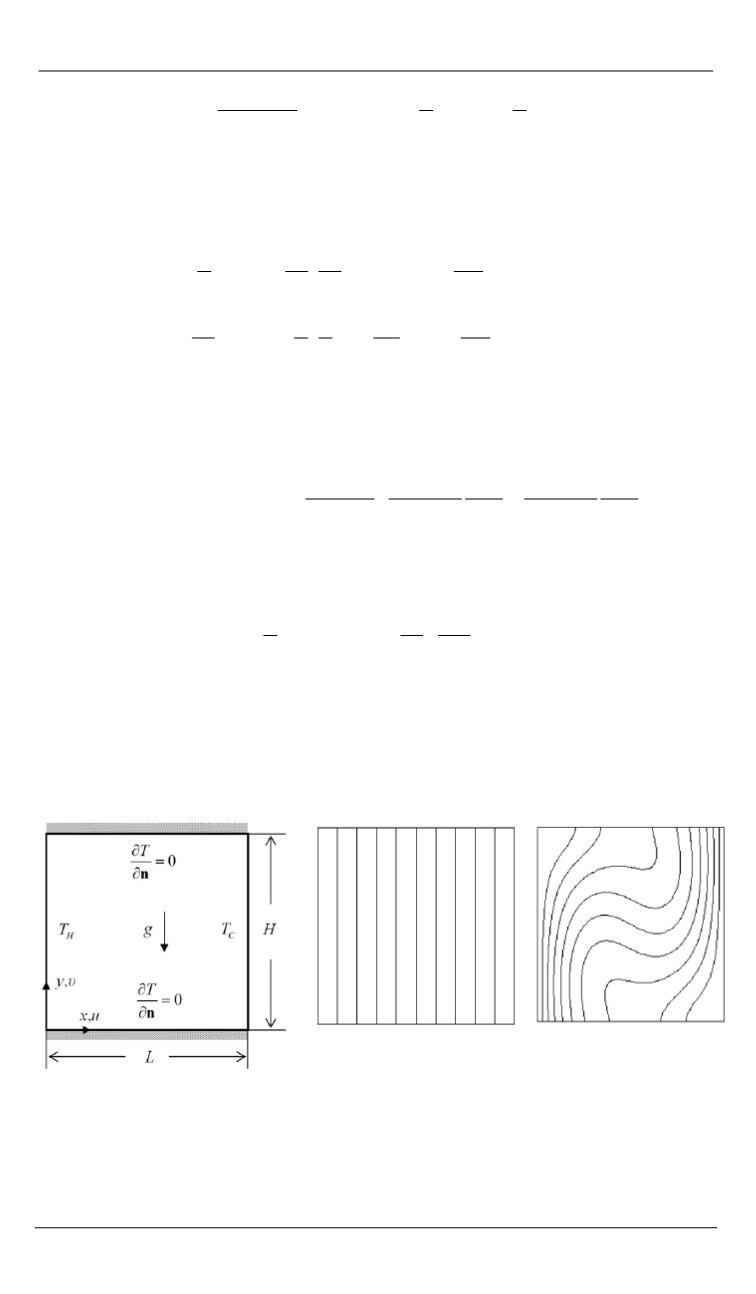
Рис. 3.
Задача конвекции с теплоизолированными верхней и нижней гранями:
а
— геометрия задачи;
б
— изолинии температуры при стационарной теплопровод-
ности;
в
— изолинии температуры при
4
Ra 10


