Решение стационарных двумерных задач естественной конвекции…
13
Для расчета квадратур в (13) используем двумерный аналог фор-
мулы трапеций на квадратной сетке 64×32 узла.
На рис. 1,
б
показано поле температуры при отсутствии конвек-
ции(
Ra 0
), а на рис. 2 приведены изолинии температуры и функции
тока в зависимости от различных значений числа Ra, которые хоро-
шо согласуются с данными работы [14].
а
б
в
г
д
е
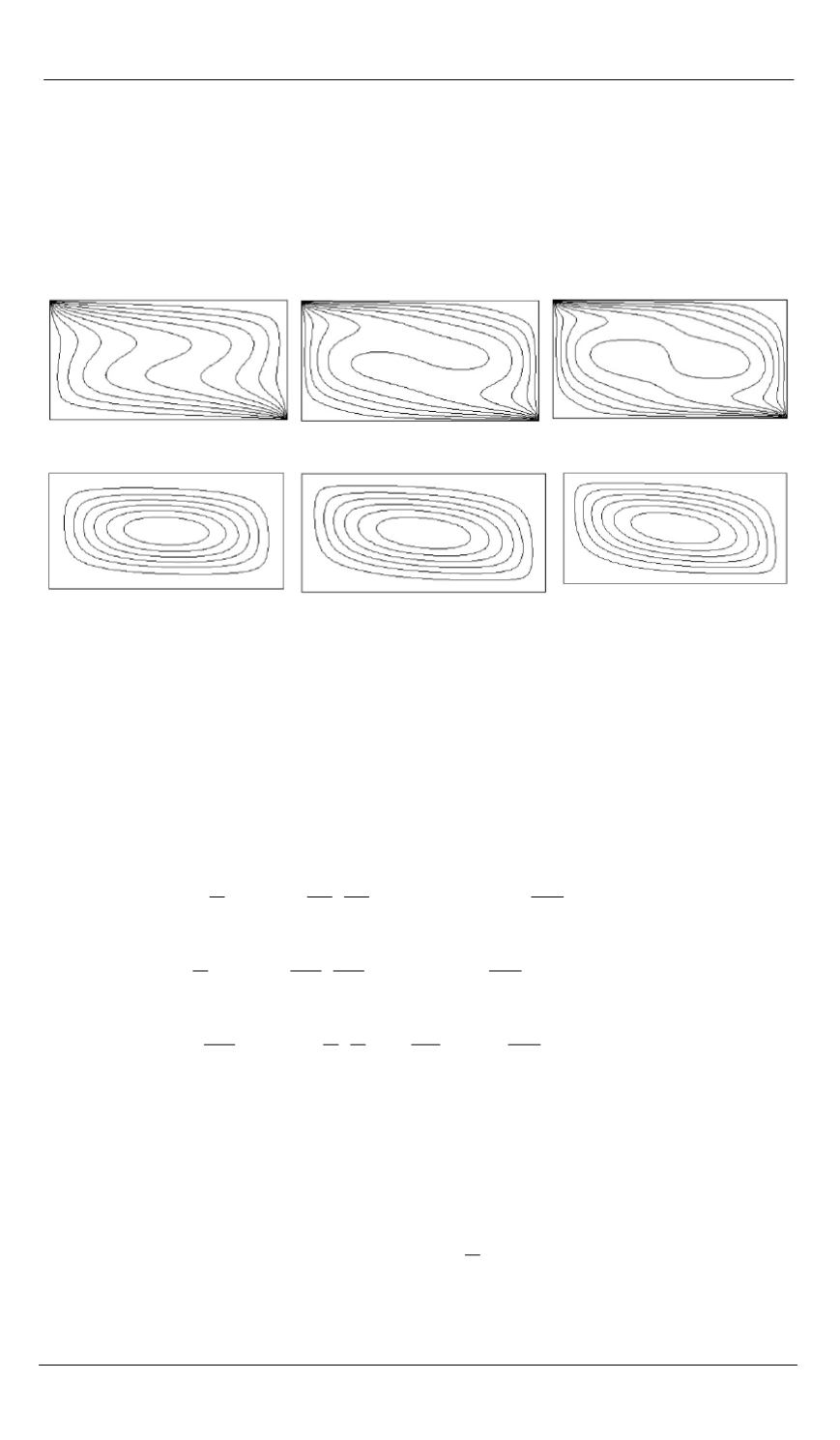
Рис. 2.
Изолинии температуры (
а — в
) и функции тока (
г — е
) при Rа =
= 10
5
(
а
,
г
); 5·10
5
(
б
,
д
); 10
6
(
в
,
е
)
Конвекция в полости со смешанными граничными условиями Ди-
рихле и Неймана.
Рассмотрим теперь хорошо изученную задачу кон-
векции в прямоугольной области, приведенную на рис. 3,
а
[13]. Для
нее имеем следующие краевые условия:
1 ,
,
:
1,
0;
2
1 ,
,
:
0;
2
2 2
1 1
,
,
:
0.
2
2 2
H H
X Y
U V
L L
H H
X Y
U V
L L
H Y
X
U V
L
n
n
n
n
(18)
С помощью обобщенной формулы Лагранжа и замены безраз-
мерной функции температуры
приведем эту задачу к задаче с од-
нородными краевыми условиями относительно
:
1
2
f
X
,
где


