Решение стационарных двумерных задач естественной конвекции…
11
( )
( )
2 ( 1)
( )
( )
( )
( )
( 1)
2 ( 1)
( )
( )
( 1)
( 1)
2 ( 1)
( 1)
( 1)
( 1)
1
;
Pr
Gr
;
;
,
.
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
U
V
S
X
Y
U
V
X
Y
X
U
V
Y
X
Здесь известные либо уже вычисленные величины записаны в
правой части выражений.
Численный эксперимент: естественная конвекция в прямо-
угольной полости.
Конвекция в полости с граничными условиями
Дирихле
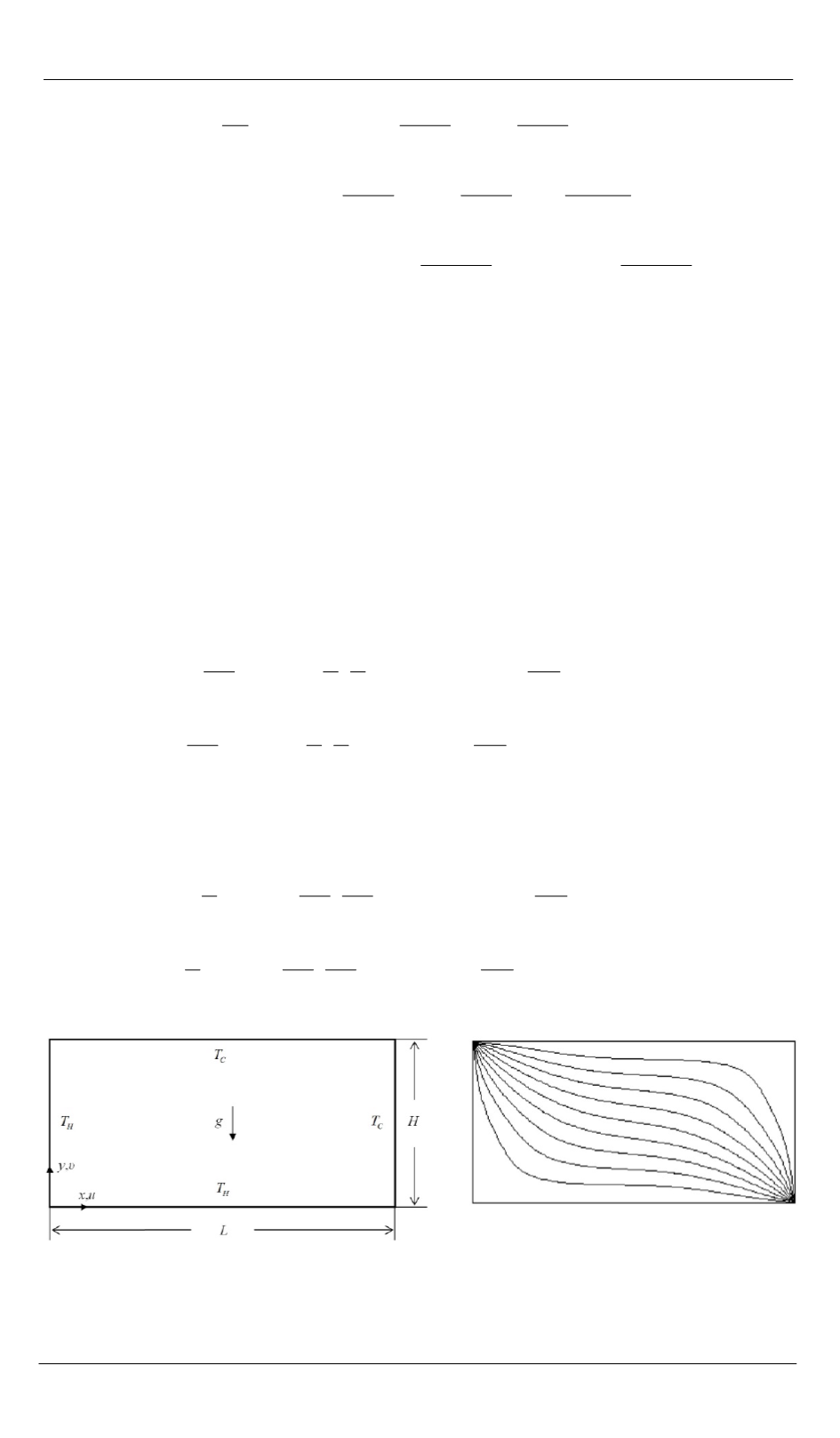
. Рассмотрим следующую задачу двумерной конвекции в по-
лости прямоугольной формы [14] (рис. 1,
а
). Задача является краевой
задачей Дирихле относительно функции температуры и описывается
системой (1) с параметрами, приведенными на с. 4. Положим начало
координат в центре области
. На нижней и верхней гранях заданы
условия
1 1
,
,
:
1,
0;
2
2 2
1 1
,
,
:
0.
2
2 2
H Y
X
U V
L
H Y
X
U V
L
n
n
Условия на левой и правой гранях следующие:
1 ,
,
:
1,
0;
2
2 2
1 ,
,
:
0.
2
2 2
H H
X Y
U V
L L
H H
X Y
U V
L L
n
n
а
б
Рис. 1.
Прямоугольная полость с граничными условиями Дирихле:
а
— геометрия задачи;
б
— изолинии температуры
(стационарная теплопроводность)


