Решение стационарных двумерных задач естественной конвекции…
15
На рис. 3,
б
и 3,
в
показаны линии уровня температуры соответ-
ственно для случаев стационарного теплопереноса при отсутствии
конвекции и при наличии конвекции в квадратной области
(
),
L H
хорошо согласующиеся с результатами [13], что также подтвержда-
ется сравнением значений числа Нуссельта Nu в различных сечениях.
Численное интегрирование проводилось методом трапеций на сетке
64 × 64 узла.
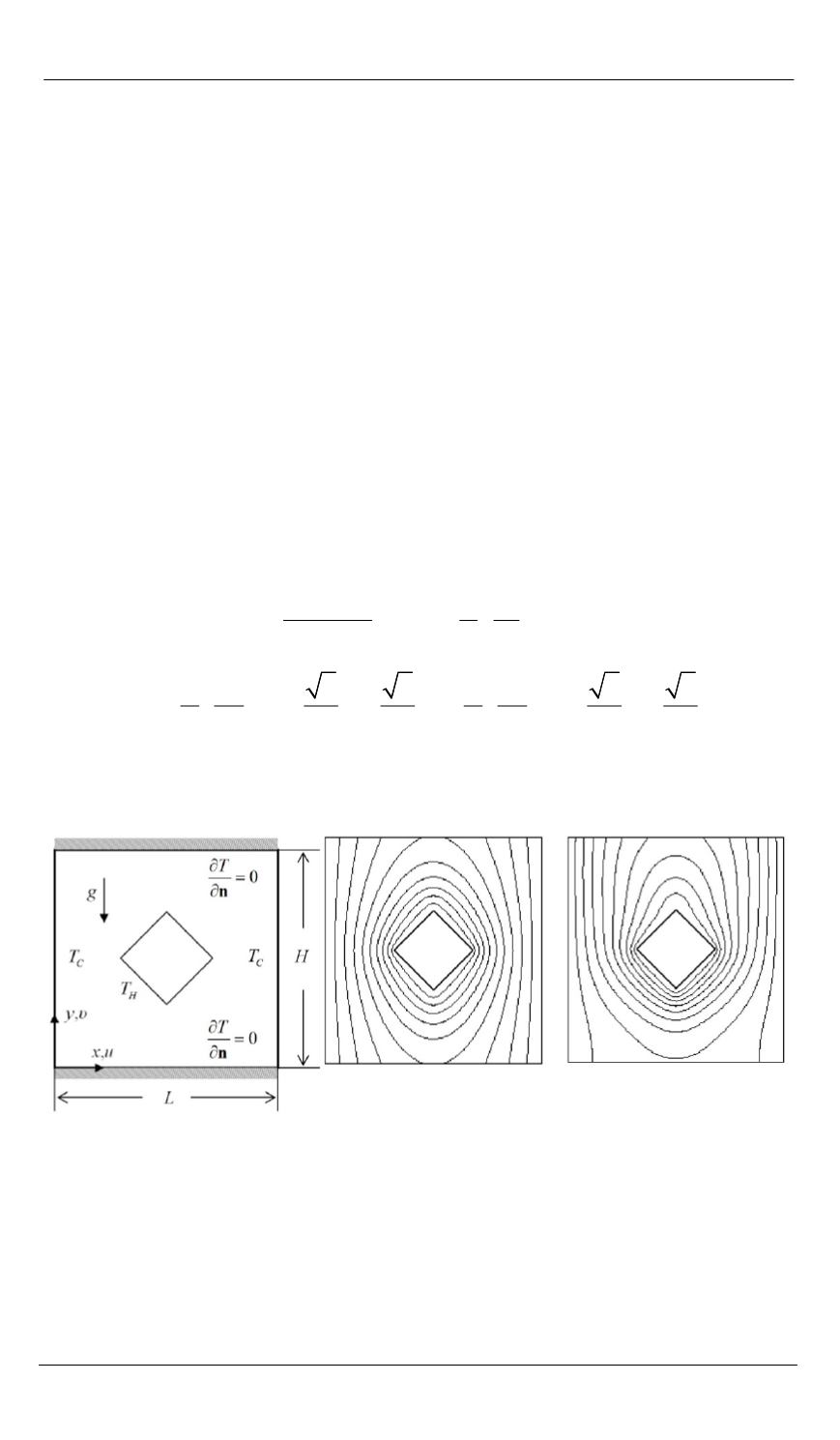
Конвекция в полости с внутренним нагревом.
Более сложный
пример, наглядно иллюстрирующий преимущества RFM, заимство-
ван из работы [15]. Геометрия задачи показана на рис. 4,
а
. В сере-
дине прямоугольной области находится внутренний призматический
источник тепла квадратного сечения. На рис. 4,
б
приведены стацио-
нарные линии уровня температуры для чистой задачи теплопровод-
ности, а на рис. 4,
в
— при наличии конвекции. Решение данной за-
дачи осуществлялось аналогично предыдущей за исключением опре-
деления функции
f
:
2
2
2
2
1
,
,
4
1
2
2 1
2
2 ,
4
2
2
4
2
2
C
C
H C
H
L
f
X
L
X Y
X Y
где
— длина стороны внутренней квадратной области.
а
б
в
Рис. 4.
Конвекция с внутренним нагревом:
а
— геометрия задачи;
б
— изолинии температуры при стационарной теплопро-
водности;
в
— изолинии температуры Ra = 10
4
Заключение.
Результаты численных экспериментов подтвержда-
ют эффективность метода
R
-функций в комбинации с методом Пет-
рова — Галеркина (PGRM) при решении задач свободной конвекции


