И.В. Станкевич
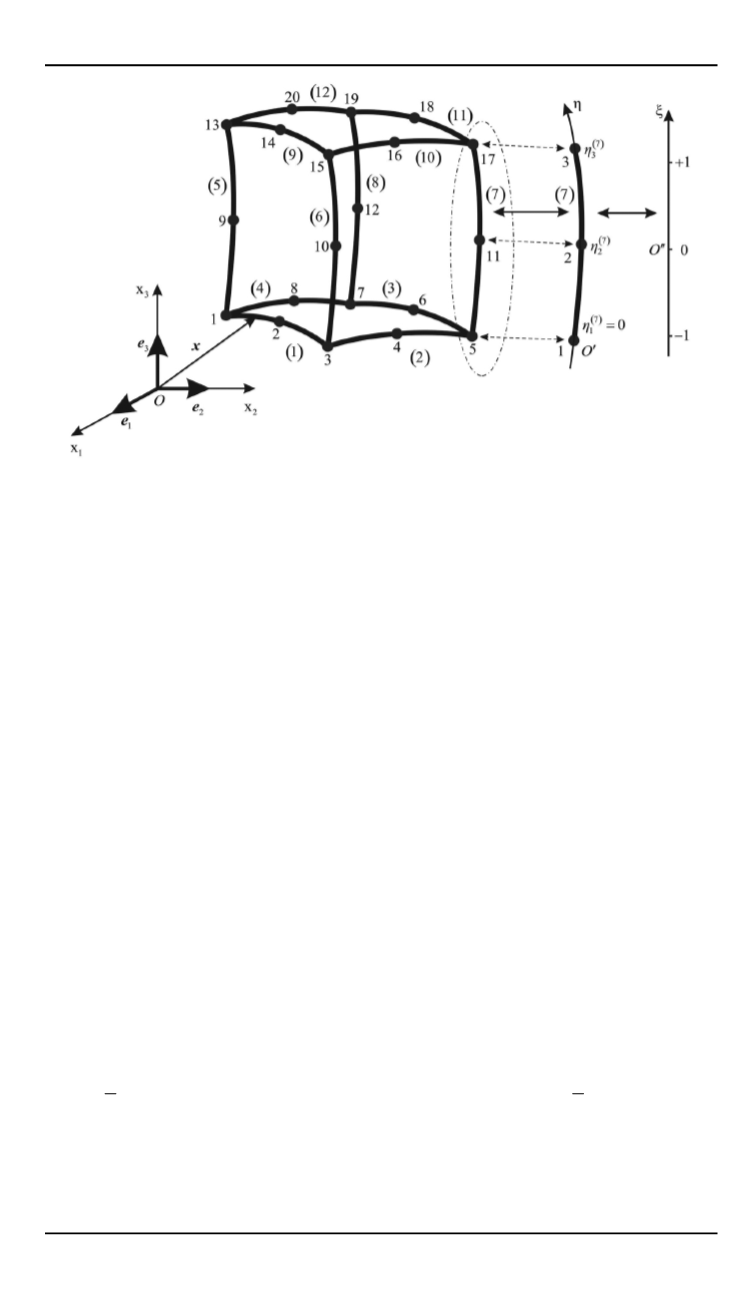
Рис. 3.
Глобальная нумерация узлов конечно-элементной модели
использовать и в том случае, когда граничные условия заданы на вы-
деленных участках боковой поверхности рассматриваемого стержня.
Для эффективной реализации процедур численного интегрирования
удобно в рассмотрение ввести так называемые поверхностные конеч-
ные элементы, которые будут аппроксимировать торцевые и боковые
поверхности стержневой системы. В дальнейшем поверхностные ко-
нечные элементы обозначены
¯
( )
. Объединение всех поверхностных
конечных элементов образует границу
ℎ
области:
ℎ
=
⋃︀
=1
¯
( )
,
где — число поверхностных элементов в сетке конечно-элементной
модели. В то же время
ℎ
=
ℎ
1
∪
ℎ
2
∪
ℎ
3
,
где
ℎ
1
,
ℎ
2
,
ℎ
3
— поверхности, аппроксимирующие поверхности
1
,
2
,
3
, на которых заданы граничные условия 1–3-го рода соответ-
ственно. Предположим, что любой поверхностный конечный элемент
¯
( )
целиком лежит на какой-либо одной поверхности. Описание этих
элементов приведено ниже.
После построения сетки конечно-элементной модели и учитывая
выражение (4), имеем функционал
F
ℎ
=
1
2
∫︁
ℎ
[︀
l
(
,
h
)
2
−
2
]︀
+
∫︁
ℎ
2
+
∫︁
ℎ
3
a
(︂
1
2
−
)︂
.
(5)
Здесь все данные, входящие в формулировку задачи (1)–(3), отнесены
к области
ℎ
и ее границе
ℎ
.
4


