И.В. Станкевич
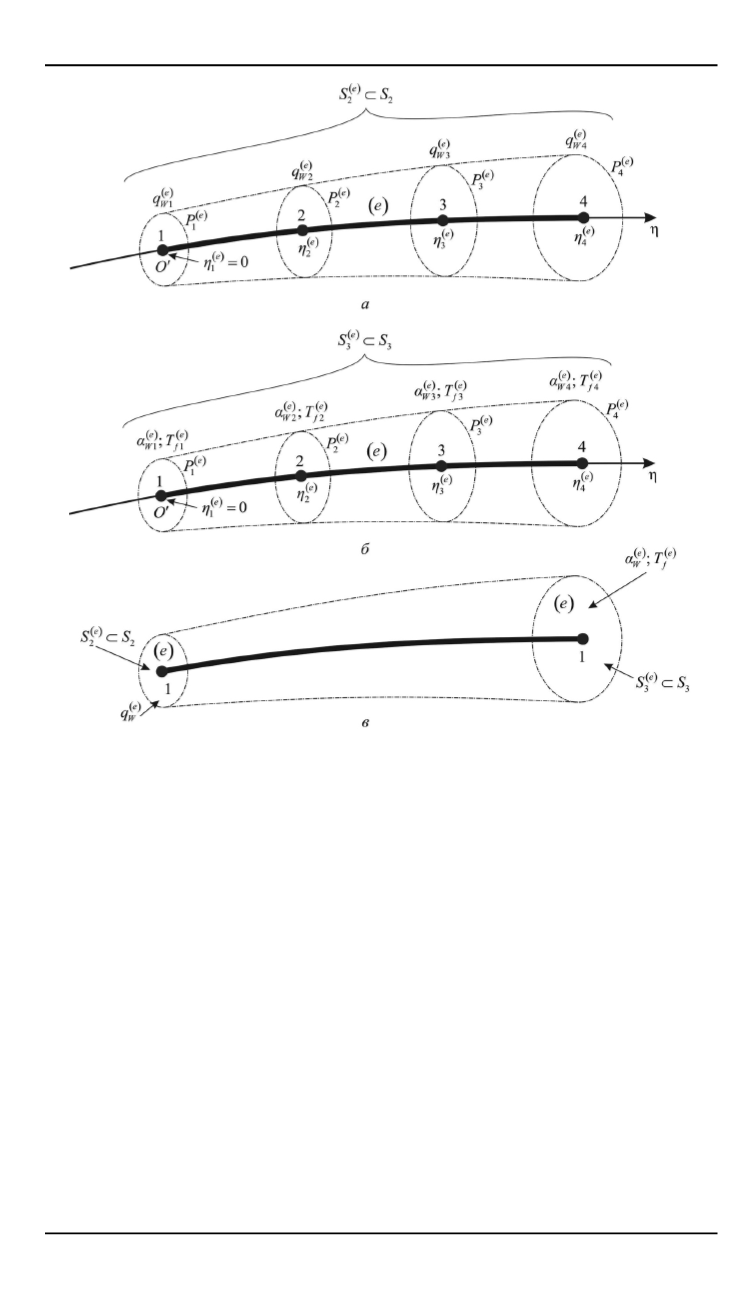
Рис. 5.
Способы задания граничных условий теплообмена
Примеры расчета температурного состояния стержневых конст-
рукций.
Изложенная выше методика математического моделирования
температурного состояния стержневых конструкций была реализо-
вана в виде комплекса прикладных программ, который применялся
для исследования ряда конструкций. Ниже представлены некоторые
результаты. На рис. 6–8 показаны стационарные температурные поля
трех вариантов пространственных стержневых конструкций, подвер-
женных симметричному (рис. 6,
а
; 7,
а
; 8,
а
) и несимметричному
тепловому нагружению (рис. 6,
б
; 7,
б
; 8,
б
). В качестве конечных
элементов были выбраны квадратичные элементы (рис. 2,
б
). В зонах
А
и
Б
на боковых поверхностях стержней были заданы граничные условия
3-го рода:
a
(
А
)
= 100
Вт
/
(
м
2
·
K
)
,
(
А
)
= 800
K и
a
(
Б
)
= 50
Вт
/
(
м
2
·
K
)
,
(
Б
)
= 500
K. Значение коэффициента теплопроводности
l
и площади
поперечных сечений всех стержней для всех конструкций были
приняты одинаковыми и равными
30
Вт
/
(
K
·
м
)
и
0
,
0001
м
2
соответ-
ственно.
14


