И.В. Станкевич
стационарной задачи теплопроводности, но с учетом предположения
о том, что в поперечных сечениях стержня отсутствуют градиенты
температуры. Имеем
l
(︀
(
h
)
,
h
)︀
,
h
+ (
h
) = 0
,
h
∈
(
h
1
,
h
2
);
(1)
l
(
h
)
,
h
|
h
=
h
1
= ;
(2)
l
(
h
)
,
h
|
h
=
h
2
=
a
(︀
−
(
h
)
)︀⃒ ⃒
h
=
h
2
,
(3)
где
l
— коэффициент теплопроводности материала стержня;
(
h
)
—
температура стержня;
(
h
)
— мощность внутренних источников (сто-
ков) теплоты;
h
1
,
h
2
— координаты торцевых поверхностей
2
и
3
стержня соответственно (
h
1
<
h
2
);
— численное значение плот-
ности теплового потока на поверхности
2
, в данном случае приня-
то, что
>
0
, если теплота отводится от поверхности
2
стержня
(
(
h
)
,
h
|
h
=
h
1
>
0
);
a
и — коэффициент теплоотдачи и температура
внешней среды вблизи поверхности
3
соответственно. Здесь и да-
лее запятой с индексом обозначена операция дифференцирования по
соответствующим координатам.
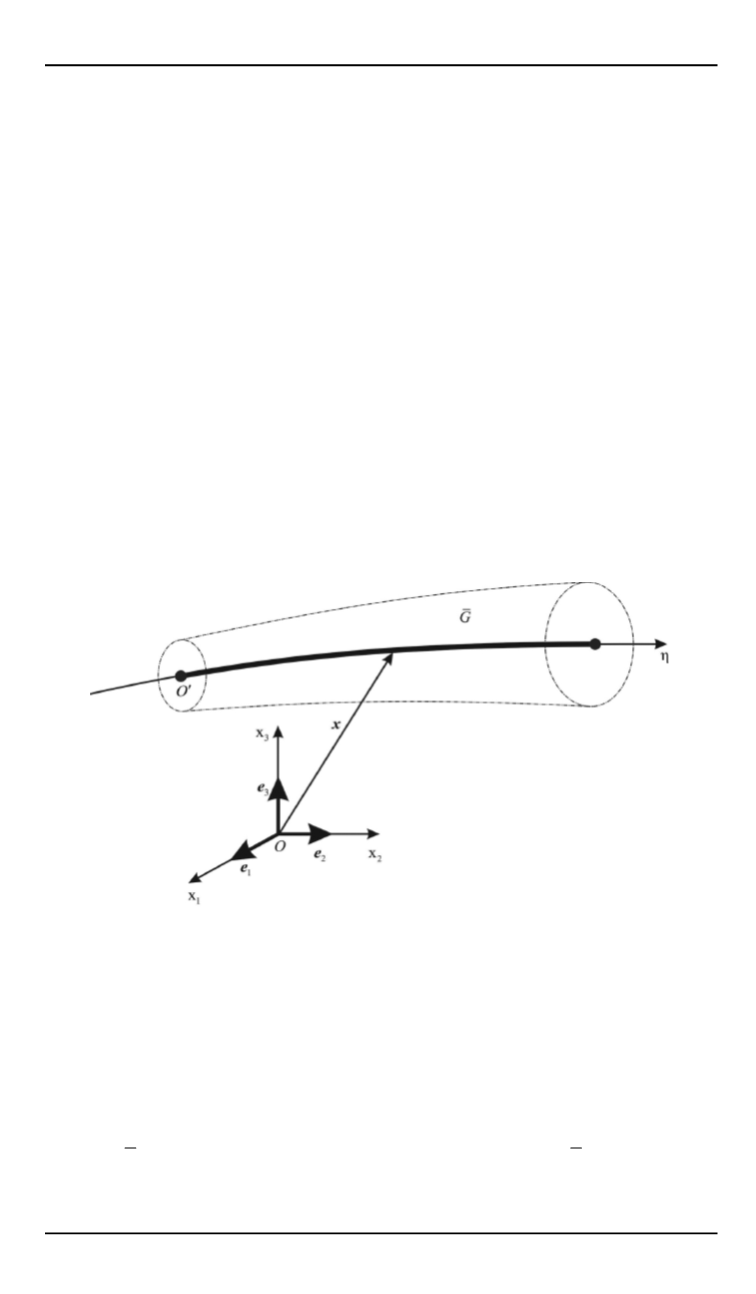
Рис. 1.
Построение пространственной криволинейной системы координат
′
h
Численное решение задачи (1)–(3) предполагает использование со-
ответствующего дискретного аналога. Построим дискретный аналог с
помощью процедур МКЭ, основанных на вариационной формулиров-
ке [5, 6]. Для этого рассмотрим функционал, имеющий следующую
структуру:
F
[ ] =
1
2
∫︁ [︀
l
(
,
h
)
2
−
2
]︀
+
∫︁
2
+
∫︁
3
a
(︂
1
2
−
)︂
.
(4)
2


