Л.Н. Лысенко, В.В. Корянов, К.Г. Райкунов
14
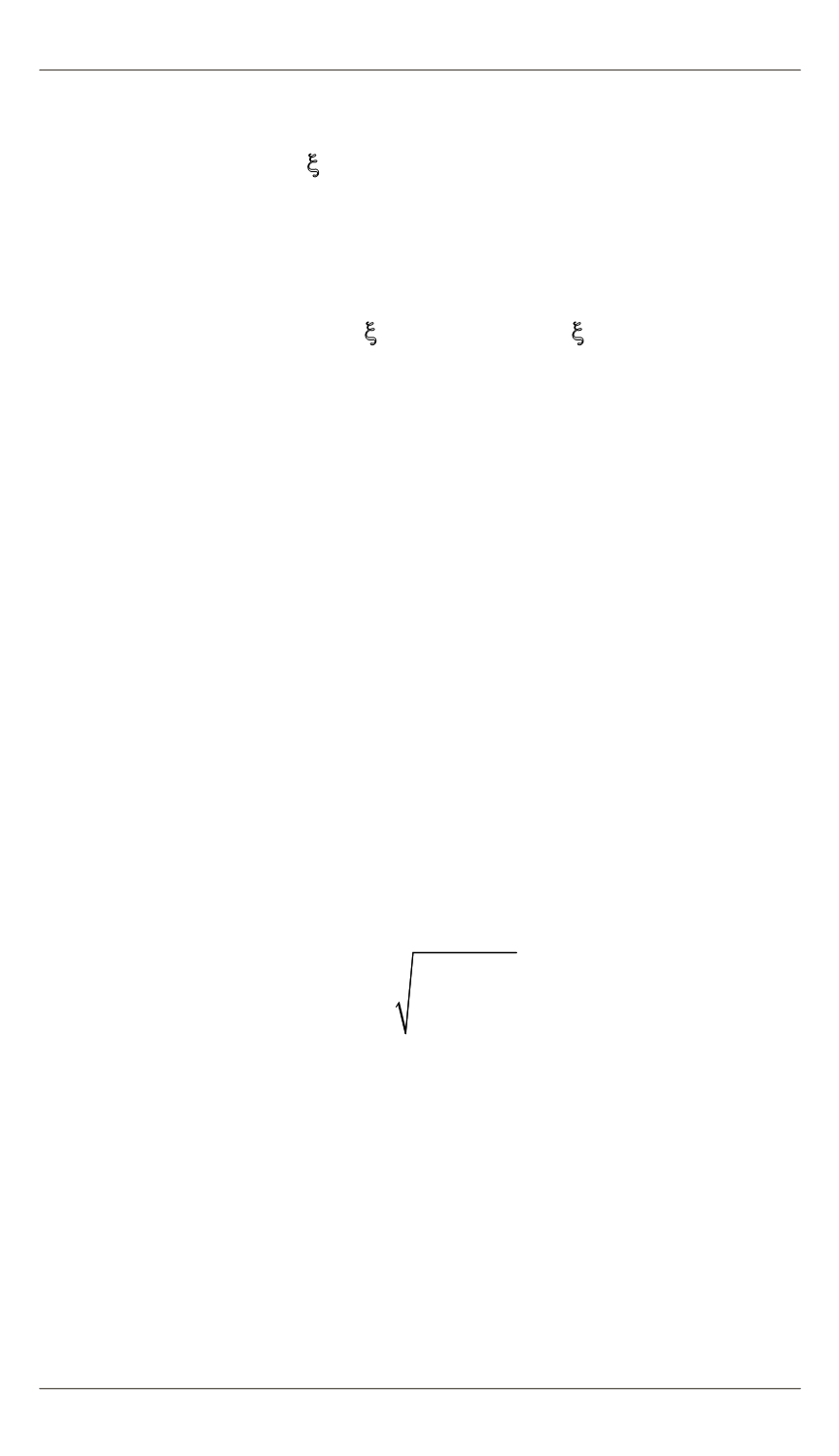
Потребуем далее, чтобы матрица
Е
(
ξ
) удовлетворяла условию
1
( )
( ) ( ),
k kj
k rj
t
t
−
=
E N N
ξ
(3)
где
1
k
−
N
— некоторая промежуточная матрица, определяемая приведен-
ной ниже формулой.
Условие (3) выполняется, если
( )
( ) ( ) ( ) ( ).
k kj
rj
rj
t
t
t
=
u
N E F G E
ξ
ξ
т
п
Используя введенную матрицу обращения
G
п
, можно получить ре-
куррентный алгоритм независимой многоразовой детерминированной
коррекции в линейной постановке, включающий операции вычисления
векторов корректирующих скоростей
u
(
t
kj
), результирующих отклоне-
ний траекторных ∆
q
(
t
kj
) и кинематических ∆
x
*
(
t
kj
) параметров после
проведения коррекции, а также величины суммарной характеристиче-
ской скорости для
п
последовательных коррекций.
1
1
1
( )
( )
( ) ( )
( ) ,
kj
k kj
kj
kj
kj
t
t
t
t
t
−
∗
−
−
=
∆
− δ
u
u N F
x
q
пр
(4)
1
1
1
1
1
( )
( ) ( )
( ) ( ) ( )
( ) ( )
( ) ,
kj
kj
kj
kj
kj
k kj
kj
kj
kj
t
t
t
t
t
t
t
t
t
∗
∗
−
−
−
∗
∗
−
−
∆ =
∆
+
+
∆
− δ
u
u
u
q
F
x
F G N F
x
q
пр
п
(5)
1
1
( )
( ) ( )
( ),
kj
kj
k kj
kj
t
t
t
t
∗
−
−
∆
=
δ
x
G N q
пр
п
(6)
6
2
6
3
( )
( ).
n
kj
i kj
i
t
u t
=
=
=
∑
u
(7)
Причем вектор отклонений корректируемых кинематических пара-
метров при расчете первой коррекции следует принимать равным ошиб-
кам выведения КА, а при последующих — в соответствии с уравнением
связи (6).
В отличие от детерминированной коррекции, в рамках моделей ко-
торой ограничиваются определением значений вектора корректирующей
скорости, предельных ошибок и энергозатрат на ее проведение, методика
расчета стохастической коррекции в общем случае должна включать
способы определения законов и параметров распределения соответству-
ющих характеристик, принимаемых случайными величинами.


