
Механика горных лыж: резаный поворот без ангуляции
Инженерный журнал: наука и инновации
# 7·2017 7
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
cos 1
sin cos
sin sin
,
1 sin cos
cos 1
sin cos
sin sin
sin ,
1 sin cos
cos 1
sin cos
sin sin
cos .
1 sin cos
A
A
ds R
d
A
A
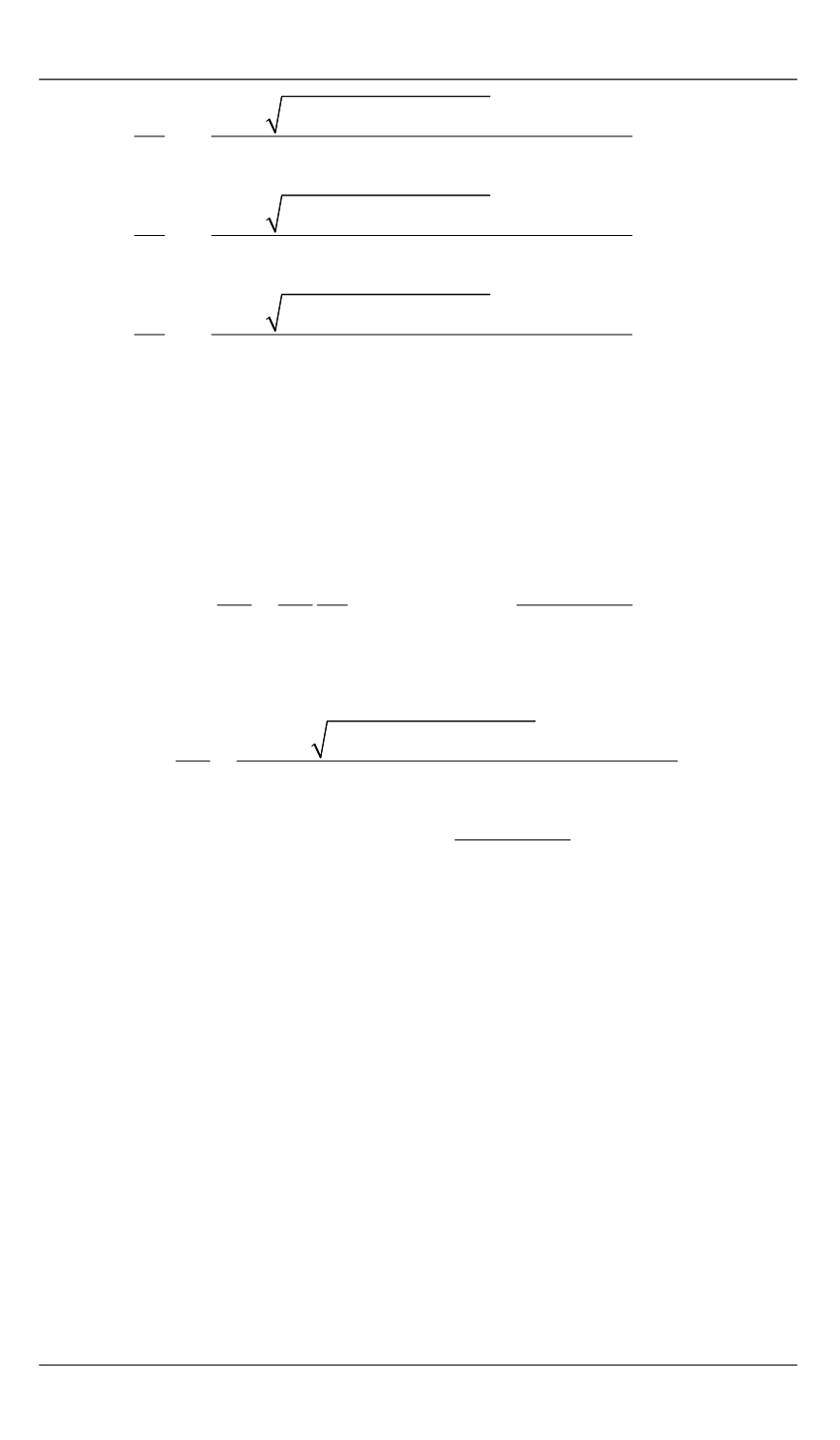
dx = R
d
A
A
dy = R
d
(20)
Из (10) следует, что величина
А
зависит от радиуса бокового вы-
реза лыжи и скорости движения. Как уже было отмечено, определе-
ние скорости движения связано с решением дифференциального
уравнения (12), которое приведем к такому виду, когда, как и в (20),
переменной величиной является угол движения
:
сопр ск
sin cos
F F
dV dV d g
dt
d dt
m
+
.
(21)
Используя (18), из (21) получаем
2
2
2
2
2
сопр ск
cos 1
sin cos
sin sin
(1 sin cos )
sin cos
.
R
A
A
dV
d
V
F F
g
m
+
(22)
Время движения
t
, скорость
V
, криволинейная координата
s
и ко-
ординаты точек траектории движения
x
,
y
как функции от значения
угла движения
могут быть найдены с учетом выражения (10) путем
численного интегрирования уравнений (18), (20), (22) при условии,
что искомые функции удовлетворяют начальным условиям, соответ-
ствующим началу отсчета движения лыжника в дуге поворота:
0
0 0
0
0
0
0
0
0
0
0
; ( )
0; ( )
0;
( )
0;
( )
0;
( )
.
t
t
s
s
x
x
y
y
V V
(23)
Задача Коши (18), (20), (22), (23) решается численно путем пошаго-
вого интегрирования, определяя на каждом шаге значения
A
,
t
,
V
,
s
,
x
и
y
.
Критические скорости движения.
Следует отметить, что реше-
ние задачи о нахождении законов движения в условиях резаного по-
ворота возможно не для всех значений начальных условий (23).
















