
С.Д. Леготин, А.А. Ривлин, В.И. Данилин
6
Инженерный журнал: наука и инновации
# 7·2017
2
2
2
2
2
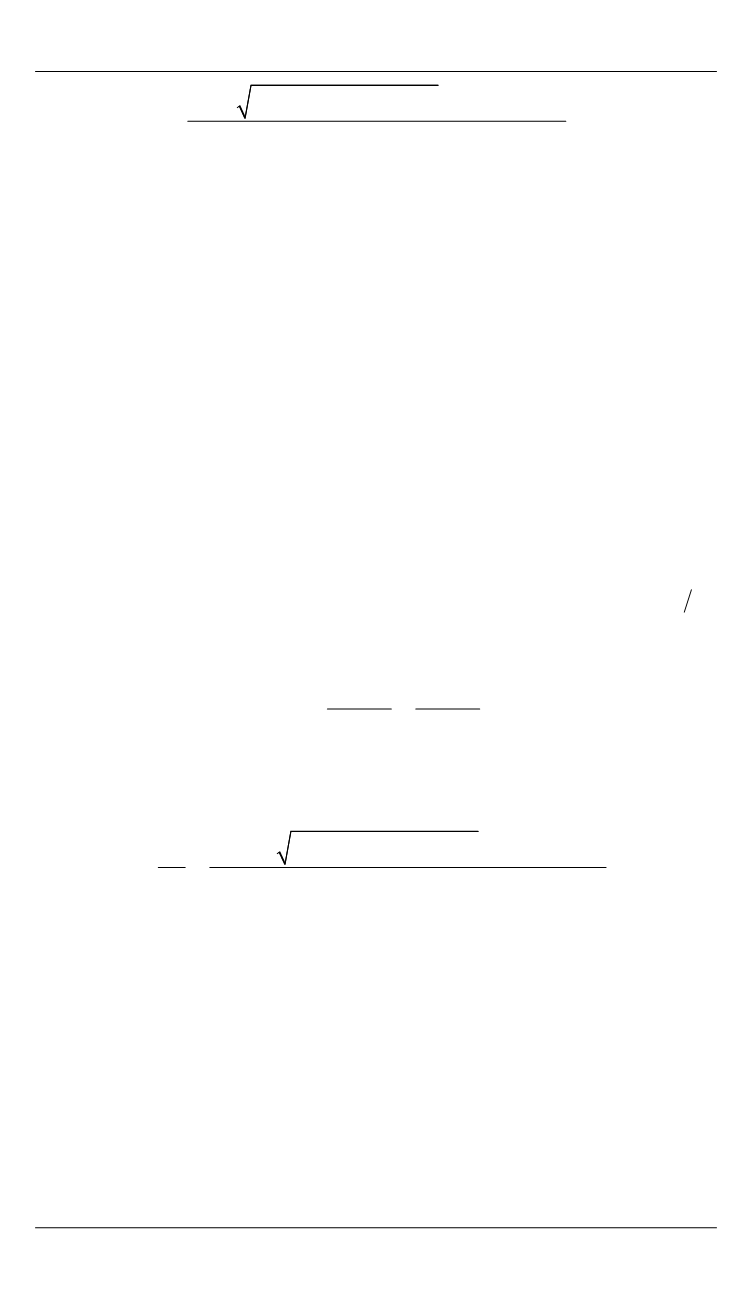
cos 1
sin cos
sin sin
cos
1 sin cos
A
A
=
.
(14)
Задача о нахождении скорости движения
V
и криволинейной ко-
ординаты
s
центра масс как функций от времени
t
путем численного
интегрирования дифференциального уравнения движения (12) реша-
лась в работах [1–4, 8]. В них начальные условия и сила аэродинами-
ческого сопротивления
сопр
F
выражаются как
0
0
0
0
0
0; ( )
;
( )
t
s t
s V t
V
,
(15)
2
сопр
в
0, 5
F
V
,
(16)
где
в
,
— плотность воздуха и аэродинамический коэффициент
соответственно.
Определим траекторию движения центра масс
С
.
Расчет движения центра масс системы лыжник — лыжи.
При
перемещении точки вдоль криволинейной координаты
s
с текущей
кривизной ρ на величину
ds
как радиус кривизны, так и перпендику-
лярный к нему вектор скорости поворачиваются на угол
d ds
.
Учитывая (8), а также условие отсутствия ангуляции, запишем изме-
нение угла движения:
cos
cos
ds
Vdt
d
R
R
.
(17)
Установим связь между временем
t
и углом движения
. Из вы-
ражения (17) с учетом (14) следует
2
2
2
2
2
cos 1
sin cos
sin sin
(1 sin cos )
R
A
A
dt
d
V
. (18)
Воспользовавшись (17), выразим элементарные перемещения
точки по естественной оси и декартовым координатам склона через
изменение угла движения:
cos ,
sin cos sin ,
cos
cos cos .
ds = R d
dx = ds
R
d
dy = ds
R
d
(19)
С учетом выражения (14) из (19) получим систему дифференци-
альных уравнений первого порядка:
















