
Механика горных лыж: резаный поворот без ангуляции
Инженерный журнал: наука и инновации
# 7·2017 11
начальный
0
60
и конечный
к
60
углы движения. Сплош-
ные линии на рис. 2 и 3 соответствуют движению центра масс (точки
С
), пунктирные — движению опорной точки (точки
О
), положение
которой определяют по траектории точки
С
, длине опорной линии,
принятой здесь равной 0,8 м, и рассчитанному углу наклона опорной
линии
(
). Положительное направление оси
x
на рис. 4 — направо
по горизонтали, оси
y
— по вертикали вверх.
В отсутствие сил сопротивления
сопр
F
и
ск
F
система уравнений
имеет полный вид (18), (20), (22), (23). На рис. 5–9 показаны результаты
численного решения задачи для таких же исходных данных, как в уже
рассмотренном примере. Различия сводятся к заданию только началь-
ной скорости движения по траектории
0
0
( )
8 м / с = 28,8 км / ч,
V V
которая затем меняется в соответствии с (22).
Сравнивая рис. 5–7 и рис. 2–4, следует отметить, что в отсутствие
диссипативных сил поворот выполняется по траектории с большей
кривизной, длина дуги снижена, при этом увеличен угол наклона
опорной линии, траектория опорной точки сильнее смещена от тра-
ектории центра масс, что связано с возрастанием скорости движения
в повороте (см. рис. 8).
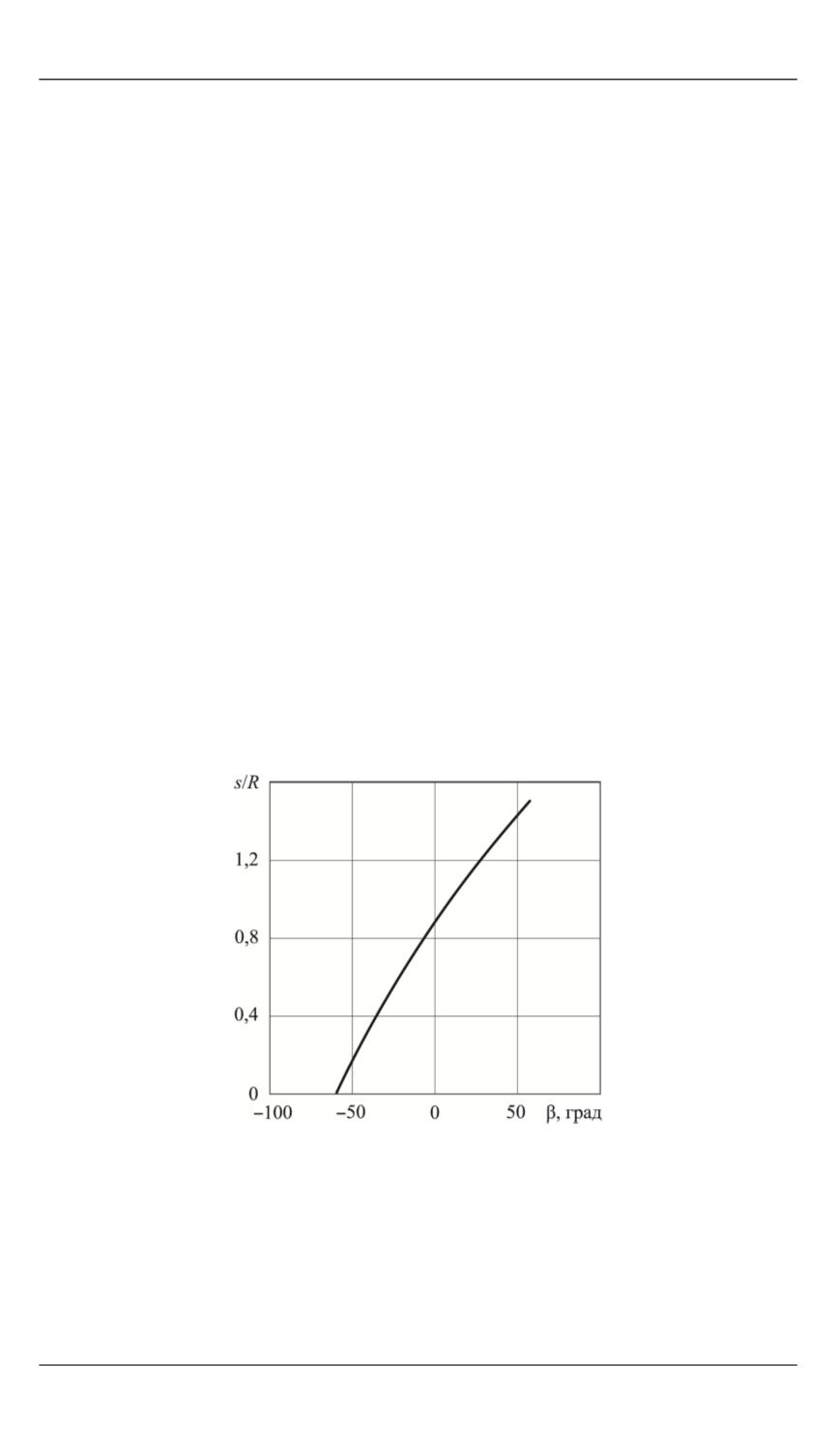
Рис. 5.
Зависимость длины дуги поворо-
та
s
центра масс, в долях
R
, от угла дви-
жения β, в отсутствие сопротивле-
ния движению
















