
Механика горных лыж: резаный поворот без ангуляции
Инженерный журнал: наука и инновации
# 7·2017 9
Если принять значения предельных углов равными
пред пред
60 ,
то на рассмотренном склоне значения предельной скорости в за-
висимости от угла движения
будут меняться в пределах 9,9…10,9 м/с
или 35,6…39,4 км/ч для слаломных и 16,2…17,9 м/с или 58…64,4 км/ч
для лыж слалома–гиганта.
Таким образом, формулируем выявленные ограничения на ско-
рость движения:
min
пред
.
V V V
Примеры решения задачи о движении без ангуляции при ре-
заном повороте.
Для численного решения полной системы уравне-
ний (18), (20), (22), (23) необходимо в (22) описывать силы сопротив-
ления движению, корректное определение которых является само-
стоятельной исследовательской задачей [4, 8, 9]. Для иллюстрации
выбранного в настоящей статье подхода численной оценки резаного
поворота в условиях отсутствия ангуляции рассмотрим два простей-
ших случая, не требующие корректного описания значений сил
сопр
F
и
ск
F
. Первый из них — движение с постоянной скоростью, второй —
отсутствие сопротивления движению.
При движении с постоянной скоростью задача сводится к инте-
грированию уравнений (18), (20) с учетом скорости
0
( )
V V
в (23).
Результаты расчета показаны на рис. 2–4. При этом были заданы сле-
дующие значения исходных данных: радиус бокового выреза
R
= 12 м,
угол склона
= 10
, скорость
0
( )
V V
= const = 8 м/с = 28,8 км/ч,
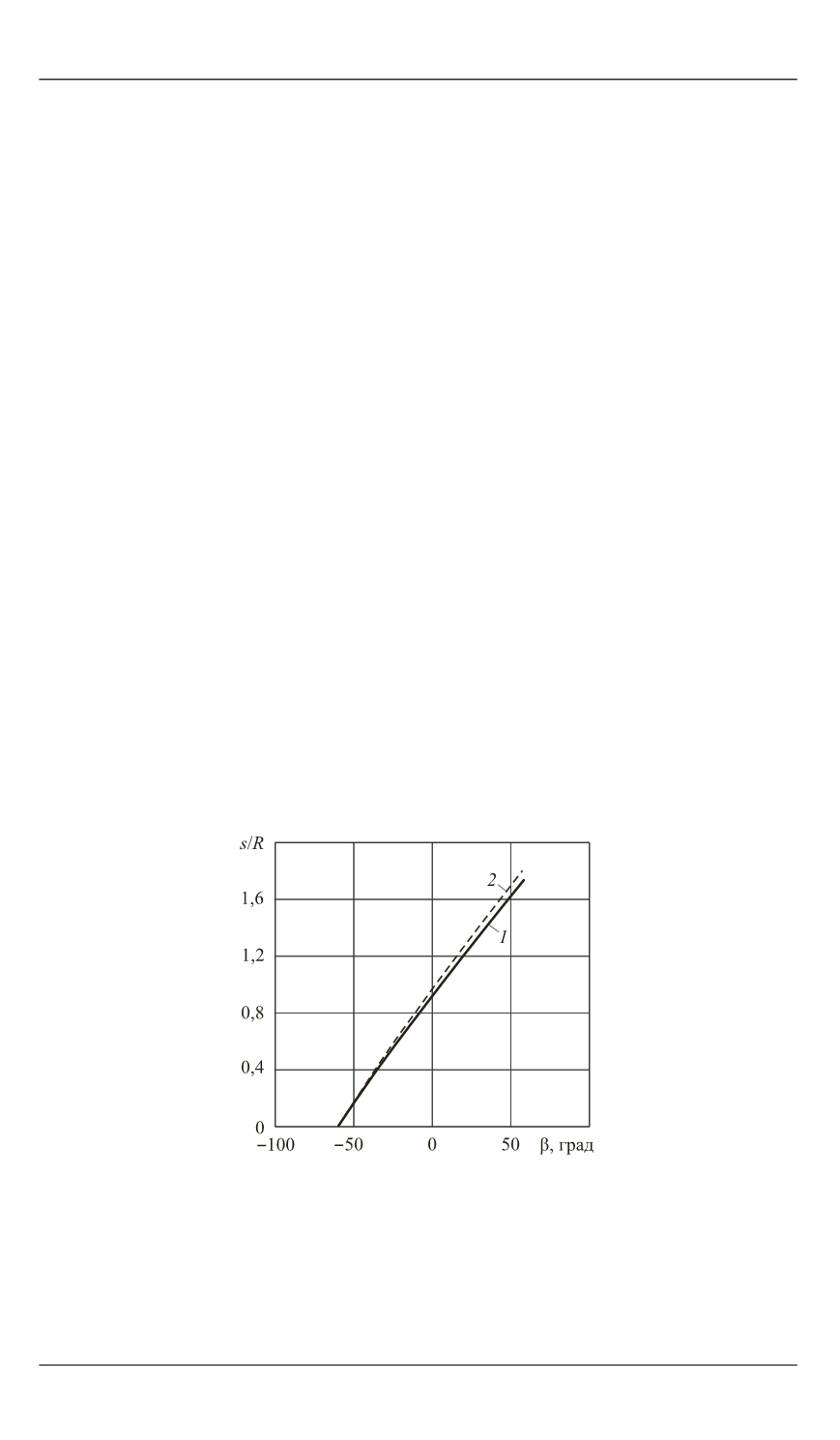
Рис. 2.
Зависимость длины дуги поворо-
та
s
,
в долях
R
, от угла движения β при
V
= const:
1
— центр масс;
2
— опорная точка
















