Н.Е. Зубов, А.В. Лапин, Е.А. Микрин
12
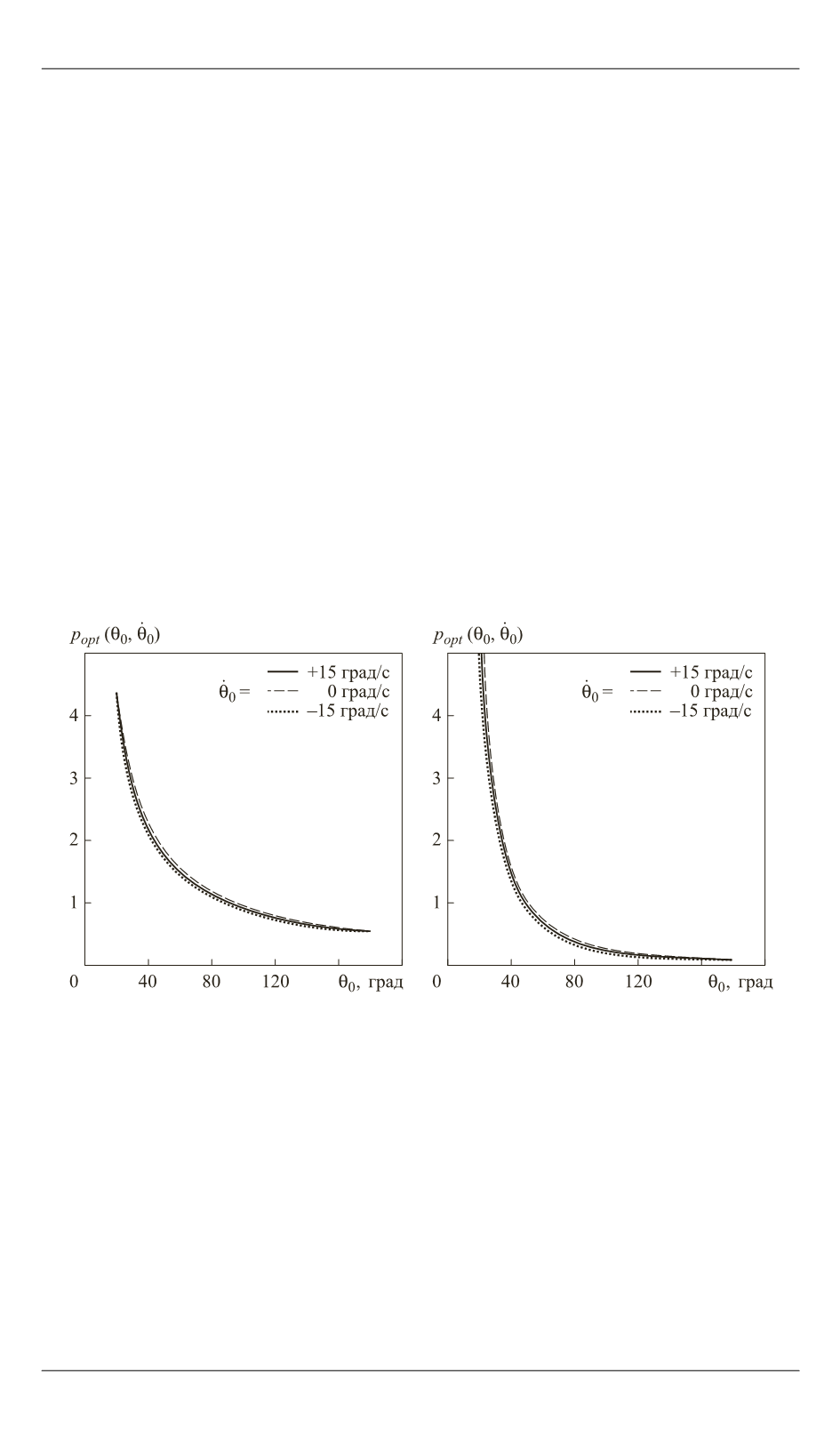
Графические зависимости, аналогичные приведенным на рис. 4,
были построены для всех начальных значений угла
θ
0
∈
[20°; 180°]
(с шагом 10°) и угловой скорости
[
]
0
15 / с; 15 / с
θ ∈ − ° + °
(с шагом
15 °/c). В результате определены значения
p
opt
и
q
opt
с точностью до
0,01 и получены функции
p
opt
(
θ
0
),
q
opt
(
θ
0
) и
T
ПП opt
(
θ
0
) для каждого из
трех значений
0
θ
(рис. 5 и 6). Анализируя графики, представленные
на рис. 5, нетрудно видеть, что при одной и той же величине
θ
0
опти-
мальные значения
p
opt
и
q
opt
для различных величин
0
θ
практически
не отличаются друг от друга. Это позволяет считать, что
(
)
(
)
opt
0 0
opt
0
,
, 0
p
p
θ θ ≈ θ
и
(
)
(
)
opt
0 0
opt
0
,
, 0
q
q
θ θ ≈ θ
. Таким образом,
p
opt
и
q
opt
являются функциями только одного аргумента
θ
0
:
p
opt
=
p
opt
(
θ
0
)
и
q
opt
=
q
opt
(
θ
0
). На практике принятое приближение может привести
лишь к тому, что наибольшее абсолютное значение угловой скорости
в течение ПП несущественно (в пределах допустимого запаса) пре-
взойдет величину
lim
θ .
Рис. 5.
Оптимальные значения
p
и
q
при различных начальных условиях
При малых начальных значениях угла
θ
0
< 20° величины
p
opt
и
q
opt
согласно изложенной методике определить затруднительно, посколь-
ку в этих случаях отсутствует четко выраженный минимум у функ-
ции
T
ПП
(
p
,
q
lim
(
p
)), вид которой показан на рис. 4. Но при таких
начальных значениях угла время ПП (рис. 6) невелико:
T
ПП
< 3 с. По-
этому важность получения точного минимума по времени ПП значи-
тельно снижается.
Далее будем аппроксимировать зависимости
p
opt
(
θ
0
) и
q
opt
(
θ
0
) сте-
пенными полиномами по критерию наименьших квадратов. Прове-


