М.Е. Третьяков
14
естествен, так как носители
S
1
,
S
2
и
S
3
не пересекаются. В соответст-
вии с оценкой
0
L
наиболее предпочтительна альтернатива (лотерея)
а
3
(L
3
).
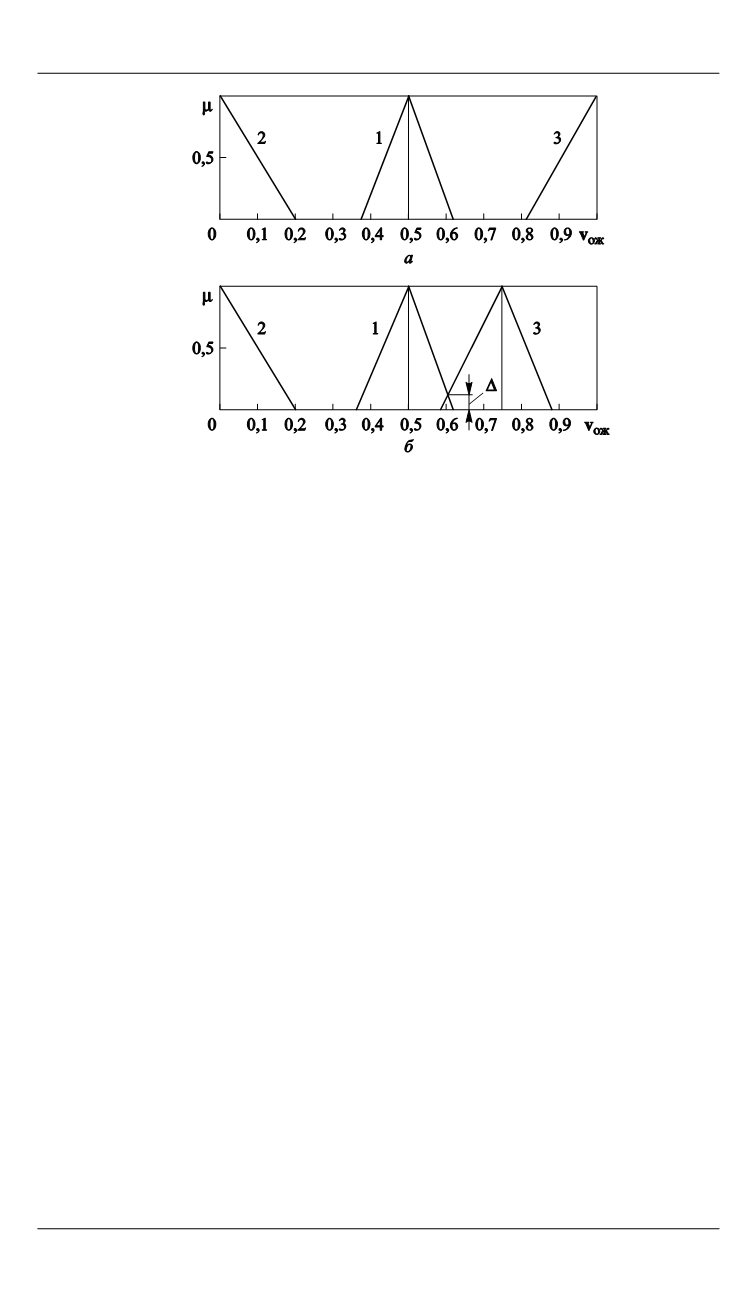
На рис. 2,
а
приведены результаты линейной аппроксимации ожи-
даемых
полезностей альтернатив (1
–
для
L
1
, 2 –
для
L
2
, 3 –
для
L
3
) для
рассмотренной выше задачи с одним изменением
–
лингвистические ве-
роятности альтернативы а3равны:
3
1
=
P
большая вероятность;
3
2
=
Р
ма-
ленькая вероятность
(номера 4, 2, см.рис. 1, б). Согласно рис. 2,
б
, нечет-
кие множества
,
,
1
2
3
ож ож ож
V V V
–
нормальные, с носителями
S
1
=(0,36, 0,61),
S
2
=(0, 0,2),
S
3
=(0,585, 0,885). В соответствии с
(20),(21) (
δ
=0,01) получено
нечеткое
множество
наиболее
предпочтительных
лотерей
{ , ;0, ;1, }
= ∆
0
1
2
3
L L L L
, где
0,1
∆ ≈
. В соответствии с величиной
0
L
наиболее предпочтительна альтернатива (лотерея)
а
3
(
L
3
).
Отметим, что аналогично можно решать подобные задачи в более
сложной постановке: большого количества траекторий
(альтернатив),
большого числа исходов альтернатив (исходом можно полагать сте-
пень ущерба причиненного МРК) и т. п.
В случае отсутствия по каким
-
либо причинам необходимой ин-
формации для расчета ожидаемых полезностей альтернатив, можно
использовать подходы, позволяющие оценить ожидаемые полезности
в порядковой шкале, что вполне достаточно для ранжирования аль-
тернатив по полезности
[5].
Выводы.
1.
Предлагается подход к решению задачи выбора тра-
ектории движения в нечеткой среде системой принятия решений
Рис. 2.
Функции принадлежности значений ожидаемых полезностей лотерей
(
альтернатив
)
в задаче выбора траектории движения МРК до цели


